weekly-contest-364
A
Statement
Metadata
- Link: 最大二进制奇数
- Difficulty: Easy
- Tag:
给你一个 二进制 字符串 s ,其中至少包含一个 '1' 。
你必须按某种方式 重新排列 字符串中的位,使得到的二进制数字是可以由该组合生成的 最大二进制奇数 。
以字符串形式,表示并返回可以由给定组合生成的最大二进制奇数。
注意 返回的结果字符串 可以 含前导零。
示例 1:
输入:s = "010"
输出:"001"
解释:因为字符串 s 中仅有一个 '1' ,其必须出现在最后一位上。所以答案是 "001" 。
示例 2:
输入:s = "0101"
输出:"1001"
解释:其中一个 '1' 必须出现在最后一位上。而由剩下的数字可以生产的最大数字是 "100" 。所以答案是 "1001" 。
提示:
1 <= s.length <= 100s仅由'0'和'1'组成s中至少包含一个'1'
Metadata
- Link: Maximum Odd Binary Number
- Difficulty: Easy
- Tag:
You are given a binary string s that contains at least one '1'.
You have to rearrange the bits in such a way that the resulting binary number is the maximum odd binary number that can be created from this combination.
Return a string representing the maximum odd binary number that can be created from the given combination.
Note that the resulting string can have leading zeros.
Example 1:
Input: s = "010"
Output: "001"
Explanation: Because there is just one '1', it must be in the last position. So the answer is "001".
Example 2:
Input: s = "0101"
Output: "1001"
Explanation: One of the '1's must be in the last position. The maximum number that can be made with the remaining digits is "100". So the answer is "1001".
Constraints:
1 <= s.length <= 100sconsists only of'0'and'1'.scontains at least one'1'.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
string maximumOddBinaryNumber(string s) {
int cnt[2] = {0, 0};
for (const auto &c : s) {
cnt[c - '0']++;
}
--cnt[1];
return std::string(cnt[1], '1') + std::string(cnt[0], '0') + "1";
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 美丽塔 I
- Difficulty: Medium
- Tag:
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山状 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山状 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j] - 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
示例 1:
输入:maxHeights = [5,3,4,1,1]
输出:13
解释:和最大的美丽塔方案为 heights = [5,3,3,1,1] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。示例 2:
输入:maxHeights = [6,5,3,9,2,7]
输出:22
解释: 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。示例 3:
输入:maxHeights = [3,2,5,5,2,3]
输出:18
解释:和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,最大值在 i = 2 处。
注意,在这个方案中,i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。
提示:
1 <= n == maxHeights <= 1031 <= maxHeights[i] <= 109
Metadata
- Link: Beautiful Towers I
- Difficulty: Medium
- Tag:
You are given a 0-indexed array maxHeights of n integers.
You are tasked with building n towers in the coordinate line. The ith tower is built at coordinate i and has a height of heights[i].
A configuration of towers is beautiful if the following conditions hold:
1 <= heights[i] <= maxHeights[i]heightsis a mountain array.
Array heights is a mountain if there exists an index i such that:
- For all
0 < j <= i,heights[j - 1] <= heights[j] - For all
i <= k < n - 1,heights[k + 1] <= heights[k]
Return the maximum possible sum of heights of a beautiful configuration of towers.
Example 1:
Input: maxHeights = [5,3,4,1,1]
Output: 13
Explanation: One beautiful configuration with a maximum sum is heights = [5,3,3,1,1]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 0.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 13.Example 2:
Input: maxHeights = [6,5,3,9,2,7]
Output: 22
Explanation: One beautiful configuration with a maximum sum is heights = [3,3,3,9,2,2]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 3.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 22.Example 3:
Input: maxHeights = [3,2,5,5,2,3]
Output: 18
Explanation: One beautiful configuration with a maximum sum is heights = [2,2,5,5,2,2]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 2.
Note that, for this configuration, i = 3 can also be considered a peak.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 18.
Constraints:
1 <= n == maxHeights <= 1031 <= maxHeights[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long maximumSumOfHeights(vector<int> &maxHeights) {
int n = int(maxHeights.size());
f = vector<ll>(n + 5, 0);
auto gao = [&](bool rev) {
int i = rev ? n : 1;
ll sum = 0;
vector<pair<int, int>> sta;
for (const auto &h : maxHeights) {
auto cur = make_pair(h, 1);
while (!sta.empty()) {
auto tmp = sta.back();
if (tmp.first > h) {
cur.second += tmp.second;
sum -= 1ll * tmp.first * tmp.second;
sta.pop_back();
} else {
break;
}
}
sta.push_back(cur);
sum += 1ll * cur.first * cur.second;
f[i] += sum;
if (rev) {
i--;
} else {
i++;
}
}
};
std::reverse(maxHeights.begin(), maxHeights.end());
gao(true);
std::reverse(maxHeights.begin(), maxHeights.end());
gao(false);
ll res = 0;
for (int i = 1; i <= n; i++) {
res = max(res, f[i] - maxHeights[i - 1]);
}
return res;
}
private:
vector<ll> f;
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 美丽塔 II
- Difficulty: Medium
- Tag:
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山状 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山状 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j] - 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
示例 1:
输入:maxHeights = [5,3,4,1,1]
输出:13
解释:和最大的美丽塔方案为 heights = [5,3,3,1,1] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。示例 2:
输入:maxHeights = [6,5,3,9,2,7]
输出:22
解释: 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。示例 3:
输入:maxHeights = [3,2,5,5,2,3]
输出:18
解释:和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组,最大值在 i = 2 处。
注意,在这个方案中,i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。
提示:
1 <= n == maxHeights <= 1051 <= maxHeights[i] <= 109
Metadata
- Link: Beautiful Towers II
- Difficulty: Medium
- Tag:
You are given a 0-indexed array maxHeights of n integers.
You are tasked with building n towers in the coordinate line. The ith tower is built at coordinate i and has a height of heights[i].
A configuration of towers is beautiful if the following conditions hold:
1 <= heights[i] <= maxHeights[i]heightsis a mountain array.
Array heights is a mountain if there exists an index i such that:
- For all
0 < j <= i,heights[j - 1] <= heights[j] - For all
i <= k < n - 1,heights[k + 1] <= heights[k]
Return the maximum possible sum of heights of a beautiful configuration of towers.
Example 1:
Input: maxHeights = [5,3,4,1,1]
Output: 13
Explanation: One beautiful configuration with a maximum sum is heights = [5,3,3,1,1]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 0.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 13.Example 2:
Input: maxHeights = [6,5,3,9,2,7]
Output: 22
Explanation: One beautiful configuration with a maximum sum is heights = [3,3,3,9,2,2]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 3.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 22.Example 3:
Input: maxHeights = [3,2,5,5,2,3]
Output: 18
Explanation: One beautiful configuration with a maximum sum is heights = [2,2,5,5,2,2]. This configuration is beautiful since:
- 1 <= heights[i] <= maxHeights[i]
- heights is a mountain of peak i = 2.
Note that, for this configuration, i = 3 can also be considered a peak.
It can be shown that there exists no other beautiful configuration with a sum of heights greater than 18.
Constraints:
1 <= n == maxHeights <= 1051 <= maxHeights[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long maximumSumOfHeights(vector<int> &maxHeights) {
int n = int(maxHeights.size());
f = vector<ll>(n + 5, 0);
auto gao = [&](bool rev) {
int i = rev ? n : 1;
ll sum = 0;
vector<pair<int, int>> sta;
for (const auto &h : maxHeights) {
auto cur = make_pair(h, 1);
while (!sta.empty()) {
auto tmp = sta.back();
if (tmp.first > h) {
cur.second += tmp.second;
sum -= 1ll * tmp.first * tmp.second;
sta.pop_back();
} else {
break;
}
}
sta.push_back(cur);
sum += 1ll * cur.first * cur.second;
f[i] += sum;
if (rev) {
i--;
} else {
i++;
}
}
};
std::reverse(maxHeights.begin(), maxHeights.end());
gao(true);
std::reverse(maxHeights.begin(), maxHeights.end());
gao(false);
ll res = 0;
for (int i = 1; i <= n; i++) {
res = max(res, f[i] - maxHeights[i - 1]);
}
return res;
}
private:
vector<ll> f;
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 统计树中的合法路径数目
- Difficulty: Hard
- Tag:
给你一棵 n 个节点的无向树,节点编号为 1 到 n 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。
请你返回树中的 合法路径数目 。
如果在节点 a 到节点 b 之间 恰好有一个 节点的编号是质数,那么我们称路径 (a, b) 是 合法的 。
注意:
- 路径
(a, b)指的是一条从节点a开始到节点b结束的一个节点序列,序列中的节点 互不相同 ,且相邻节点之间在树上有一条边。 - 路径
(a, b)和路径(b, a)视为 同一条 路径,且只计入答案 一次 。
示例 1:
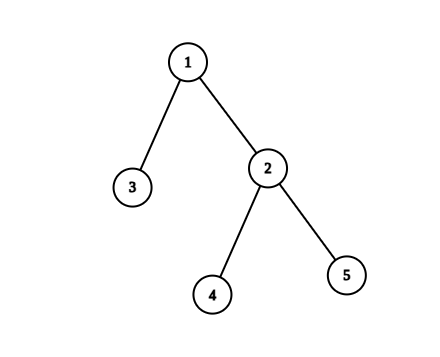
输入:n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
输出:4
解释:恰好有一个质数编号的节点路径有:
- (1, 2) 因为路径 1 到 2 只包含一个质数 2 。
- (1, 3) 因为路径 1 到 3 只包含一个质数 3 。
- (1, 4) 因为路径 1 到 4 只包含一个质数 2 。
- (2, 4) 因为路径 2 到 4 只包含一个质数 2 。
只有 4 条合法路径。
示例 2:
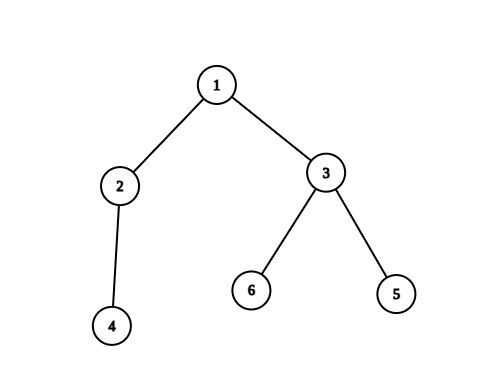
输入:n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
输出:6
解释:恰好有一个质数编号的节点路径有:
- (1, 2) 因为路径 1 到 2 只包含一个质数 2 。
- (1, 3) 因为路径 1 到 3 只包含一个质数 3 。
- (1, 4) 因为路径 1 到 4 只包含一个质数 2 。
- (1, 6) 因为路径 1 到 6 只包含一个质数 3 。
- (2, 4) 因为路径 2 到 4 只包含一个质数 2 。
- (3, 6) 因为路径 3 到 6 只包含一个质数 3 。
只有 6 条合法路径。
提示:
1 <= n <= 105edges.length == n - 1edges[i].length == 21 <= ui, vi <= n- 输入保证
edges形成一棵合法的树。
Metadata
- Link: Count Valid Paths in a Tree
- Difficulty: Hard
- Tag:
There is an undirected tree with n nodes labeled from 1 to n. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree.
Return the number of valid paths in the tree.
A path (a, b) is valid if there exists exactly one prime number among the node labels in the path from a to b.
Note that:
- The path
(a, b)is a sequence of distinct nodes starting with nodeaand ending with nodebsuch that every two adjacent nodes in the sequence share an edge in the tree. - Path
(a, b)and path(b, a)are considered the same and counted only once.
Example 1:

Input: n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
Output: 4
Explanation: The pairs with exactly one prime number on the path between them are:
- (1, 2) since the path from 1 to 2 contains prime number 2.
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (2, 4) since the path from 2 to 4 contains prime number 2.
It can be shown that there are only 4 valid paths.
Example 2:

Input: n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
Output: 6
Explanation: The pairs with exactly one prime number on the path between them are:
- (1, 2) since the path from 1 to 2 contains prime number 2.
- (1, 3) since the path from 1 to 3 contains prime number 3.
- (1, 4) since the path from 1 to 4 contains prime number 2.
- (1, 6) since the path from 1 to 6 contains prime number 3.
- (2, 4) since the path from 2 to 4 contains prime number 2.
- (3, 6) since the path from 3 to 6 contains prime number 3.
It can be shown that there are only 6 valid paths.
Constraints:
1 <= n <= 105edges.length == n - 1edges[i].length == 21 <= ui, vi <= n- The input is generated such that
edgesrepresent a valid tree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 1e5 + 20;
int pri[N], check[N];
void sieve() {
memset(check, 0, sizeof check);
check[1] = 1;
*pri = 0;
for (int i = 2; i < N; ++i) {
if (!check[i]) {
pri[++*pri] = i;
}
for (int j = 1; j <= *pri; ++j) {
if (1ll * i * pri[j] >= N)
break;
check[i * pri[j]] = 1;
if (i % pri[j] == 0)
break;
}
}
}
class Solution {
public:
void dfs(int u, int fa) {
if (!check[u]) {
f[u][0] = 0;
f[u][1] = 1;
} else {
f[u][0] = 1;
f[u][1] = 0;
}
for (const auto &v : G[u]) {
if (v == fa) {
continue;
}
dfs(v, u);
if (!check[u]) {
f[u][1] += f[v][0];
} else {
f[u][0] += f[v][0];
f[u][1] += f[v][1];
}
}
}
void dfs1(int u, int fa) {
// if (!check[u]) {
// g[u][0] += 0;
// g[u][1] += 1;
// } else {
// g[u][0] += 1;
// g[u][1] += 0;
// }
for (const auto &v : G[u]) {
if (v == fa) {
continue;
}
if (!check[v]) {
g[v][1] += g[u][0] + f[u][0] - f[v][0];
} else {
g[v][0] += g[u][0] + f[u][0] - f[v][0];
g[v][1] += g[u][1] + f[u][1] - f[v][1];
}
dfs1(v, u);
}
}
long long countPaths(int n, vector<vector<int>> &edges) {
this->n = n;
clear();
if (n == 1) {
return 0;
}
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1, 0);
// g[1][0] = 1;
dfs1(1, 0);
for (int i = 1; i <= n; i++) {
res += f[i][1];
res += g[i][1];
// cout << i << " " << f[i][0] << " " << f[i][1] << " " << g[i][0] << " " << g[i][1] << endl;
}
res /= 2;
for (int i = 2; i <= n; i++) {
if (!check[i]) {
--res;
}
}
return res;
}
private:
void clear() {
if (!load_sieve) {
sieve();
load_sieve = true;
}
for (int i = 0; i <= n + 5; i++) {
f[i][0] = 0;
f[i][1] = 0;
g[i][0] = 0;
g[i][1] = 0;
}
res = 0;
G = vector<vector<int>>(n + 5, vector<int>());
}
int n;
vector<vector<int>> G;
ll res, f[N][2], g[N][2];
bool load_sieve{false};
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
Solution1
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 1e5 + 20;
int pri[N], check[N];
void sieve() {
memset(check, 0, sizeof check);
check[1] = 1;
*pri = 0;
for (int i = 2; i < N; ++i) {
if (!check[i]) {
pri[++*pri] = i;
}
for (int j = 1; j <= *pri; ++j) {
if (1ll * i * pri[j] >= N)
break;
check[i * pri[j]] = 1;
if (i % pri[j] == 0)
break;
}
}
}
class Solution {
public:
void dfs(int u, int fa) {
if (!check[u]) {
f[u][0] = 0;
f[u][1] = 1;
} else {
f[u][0] = 1;
f[u][1] = 0;
}
for (const auto &v : G[u]) {
if (v == fa) {
continue;
}
dfs(v, u);
res += f[u][0] * f[v][1];
res += f[u][1] * f[v][0];
if (!check[u]) {
f[u][1] += f[v][0];
} else {
f[u][0] += f[v][0];
f[u][1] += f[v][1];
}
}
}
long long countPaths(int n, vector<vector<int>> &edges) {
this->n = n;
clear();
if (n == 1) {
return 0;
}
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1, 0);
return res;
}
private:
void clear() {
if (!load_sieve) {
sieve();
load_sieve = true;
}
for (int i = 0; i <= n + 5; i++) {
f[i][0] = 0;
f[i][1] = 0;
}
res = 0;
G = vector<vector<int>>(n + 5, vector<int>());
}
int n;
vector<vector<int>> G;
ll res, f[N][2];
bool load_sieve{false};
};
#ifdef LOCAL
int main() {
return 0;
}
#endif