weekly-contest-286
A
Statement
Metadata
- Link: 找出两数组的不同
- Difficulty: Easy
- Tag:
数组哈希表
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,请你返回一个长度为 2 的列表 answer ,其中:
answer[0]是nums1中所有 不 存在于nums2中的 不同 整数组成的列表。answer[1]是nums2中所有 不 存在于nums1中的 不同 整数组成的列表。
注意:列表中的整数可以按 任意 顺序返回。
示例 1:
输入:nums1 = [1,2,3], nums2 = [2,4,6]
输出:[[1,3],[4,6]]
解释:
对于 nums1 ,nums1[1] = 2 出现在 nums2 中下标 0 处,然而 nums1[0] = 1 和 nums1[2] = 3 没有出现在 nums2 中。因此,answer[0] = [1,3]。
对于 nums2 ,nums2[0] = 2 出现在 nums1 中下标 1 处,然而 nums2[1] = 4 和 nums2[2] = 6 没有出现在 nums2 中。因此,answer[1] = [4,6]。示例 2:
输入:nums1 = [1,2,3,3], nums2 = [1,1,2,2]
输出:[[3],[]]
解释:
对于 nums1 ,nums1[2] 和 nums1[3] 没有出现在 nums2 中。由于 nums1[2] == nums1[3] ,二者的值只需要在 answer[0] 中出现一次,故 answer[0] = [3]。
nums2 中的每个整数都在 nums1 中出现,因此,answer[1] = [] 。
提示:
1 <= nums1.length, nums2.length <= 1000-1000 <= nums1[i], nums2[i] <= 1000
Metadata
- Link: Find the Difference of Two Arrays
- Difficulty: Easy
- Tag:
ArrayHash Table
Given two 0-indexed integer arrays nums1 and nums2, return a list answer of size 2 where:
answer[0]is a list of all distinct integers innums1which are not present innums2.answer[1]is a list of all distinct integers innums2which are not present innums1.
Note that the integers in the lists may be returned in any order.
Example 1:
Input: nums1 = [1,2,3], nums2 = [2,4,6]
Output: [[1,3],[4,6]]
Explanation:
For nums1, nums1[1] = 2 is present at index 0 of nums2, whereas nums1[0] = 1 and nums1[2] = 3 are not present in nums2. Therefore, answer[0] = [1,3].
For nums2, nums2[0] = 2 is present at index 1 of nums1, whereas nums2[1] = 4 and nums2[2] = 6 are not present in nums2. Therefore, answer[1] = [4,6].Example 2:
Input: nums1 = [1,2,3,3], nums2 = [1,1,2,2]
Output: [[3],[]]
Explanation:
For nums1, nums1[2] and nums1[3] are not present in nums2. Since nums1[2] == nums1[3], their value is only included once and answer[0] = [3].
Every integer in nums2 is present in nums1. Therefore, answer[1] = [].
Constraints:
1 <= nums1.length, nums2.length <= 1000-1000 <= nums1[i], nums2[i] <= 1000
Solution
B
Statement
Metadata
- Link: 美化数组的最少删除数
- Difficulty: Medium
- Tag:
栈贪心数组
给你一个下标从 0 开始的整数数组 nums ,如果满足下述条件,则认为数组 nums 是一个 美丽数组 :
nums.length为偶数- 对所有满足
i % 2 == 0的下标i,nums[i] != nums[i + 1]均成立
注意,空数组同样认为是美丽数组。
你可以从 nums 中删除任意数量的元素。当你删除一个元素时,被删除元素右侧的所有元素将会向左移动一个单位以填补空缺,而左侧的元素将会保持 不变 。
返回使 nums 变为美丽数组所需删除的 最少 元素数目。
示例 1:
输入:nums = [1,1,2,3,5]
输出:1
解释:可以删除 nums[0] 或 nums[1] ,这样得到的 nums = [1,2,3,5] 是一个美丽数组。可以证明,要想使 nums 变为美丽数组,至少需要删除 1 个元素。示例 2:
输入:nums = [1,1,2,2,3,3]
输出:2
解释:可以删除 nums[0] 和 nums[5] ,这样得到的 nums = [1,2,2,3] 是一个美丽数组。可以证明,要想使 nums 变为美丽数组,至少需要删除 2 个元素。
提示:
1 <= nums.length <= 1050 <= nums[i] <= 105
Metadata
- Link: Minimum Deletions to Make Array Beautiful
- Difficulty: Medium
- Tag:
StackGreedyArray
You are given a 0-indexed integer array nums. The array nums is beautiful if:
nums.lengthis even.nums[i] != nums[i + 1]for alli % 2 == 0.
Note that an empty array is considered beautiful.
You can delete any number of elements from nums. When you delete an element, all the elements to the right of the deleted element will be shifted one unit to the left to fill the gap created and all the elements to the left of the deleted element will remain unchanged.
Return the minimum number of elements to delete from nums to make it beautiful.
Example 1:
Input: nums = [1,1,2,3,5]
Output: 1
Explanation: You can delete either nums[0] or nums[1] to make nums = [1,2,3,5] which is beautiful. It can be proven you need at least 1 deletion to make nums beautiful.
Example 2:
Input: nums = [1,1,2,2,3,3]
Output: 2
Explanation: You can delete nums[0] and nums[5] to make nums = [1,2,2,3] which is beautiful. It can be proven you need at least 2 deletions to make nums beautiful.
Constraints:
1 <= nums.length <= 1050 <= nums[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minDeletion(vector<int> &nums) {
int n = nums.size();
int i = 0;
for (int j = 1; j < n; j++) {
if (i % 2 == 0 && nums[j] == nums[i]) {
continue;
}
nums[++i] = nums[j];
}
if (i % 2 == 0) {
--i;
}
return n - (i + 1);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 找到指定长度的回文数
- Difficulty: Medium
- Tag:
数组数学
给你一个整数数组 queries 和一个 正 整数 intLength ,请你返回一个数组 answer ,其中 answer[i] 是长度为 intLength 的 正回文数 中第 queries[i] 小的数字,如果不存在这样的回文数,则为 -1 。
回文数 指的是从前往后和从后往前读一模一样的数字。回文数不能有前导 0 。
示例 1:
输入:queries = [1,2,3,4,5,90], intLength = 3
输出:[101,111,121,131,141,999]
解释:
长度为 3 的最小回文数依次是:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, …
第 90 个长度为 3 的回文数是 999 。
示例 2:
输入:queries = [2,4,6], intLength = 4
输出:[1111,1331,1551]
解释:
长度为 4 的前 6 个回文数是:
1001, 1111, 1221, 1331, 1441 和 1551 。
提示:
1 <= queries.length <= 5 * 1041 <= queries[i] <= 1091 <= intLength <= 15
Metadata
- Link: Find Palindrome With Fixed Length
- Difficulty: Medium
- Tag:
ArrayMath
Given an integer array queries and a positive integer intLength, return an array answer where answer[i] is either the queries[i]th smallest positive palindrome of length intLength or -1 if no such palindrome exists.
A palindrome is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
Example 1:
Input: queries = [1,2,3,4,5,90], intLength = 3
Output: [101,111,121,131,141,999]
Explanation:
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, …
The 90th palindrome of length 3 is 999.
Example 2:
Input: queries = [2,4,6], intLength = 4
Output: [1111,1331,1551]
Explanation:
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
Constraints:
1 <= queries.length <= 5 * 1041 <= queries[i] <= 1091 <= intLength <= 15
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long Max(int n) {
long long res = 0;
for (int i = 0; i < n; i++) {
res = res * 10 + 9;
}
return res;
}
long long Min(int n) {
long long res = 1;
for (int i = 1; i < n; i++) {
res *= 10;
}
return res;
}
long long Make(long long tar, int flag) {
string s = to_string(tar);
int len = s.length();
for (int i = len - 1 - flag; i >= 0; i--) {
s += s[i];
}
long long res = 0;
for (int i = 0; i < s.length(); i++) {
res = res * 10 + (s[i] - '0');
}
return res;
}
vector<long long> kthPalindrome(vector<int> &queries, int intLength) {
int q = queries.size();
auto res = vector<long long>(q, 0);
for (int i = 0; i < q; i++) {
int len = (intLength + 1) / 2;
long long r = Max(len);
long long l = Min(len);
// cout << l << " " << r << endl;
long long tot = (r - l + 1);
if (queries[i] > tot) {
res[i] = -1;
continue;
}
long long tar = l + queries[i] - 1;
res[i] = Make(tar, intLength & 1);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 从栈中取出 K 个硬币的最大面值和
- Difficulty: Hard
- Tag:
数组动态规划前缀和
一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。
每一次操作中,你可以从任意一个栈的 顶部 取出 1 个硬币,从栈中移除它,并放入你的钱包里。
给你一个列表 piles ,其中 piles[i] 是一个整数数组,分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ,请你返回在 恰好 进行 k 次操作的前提下,你钱包里硬币面值之和 最大为多少 。
示例 1:
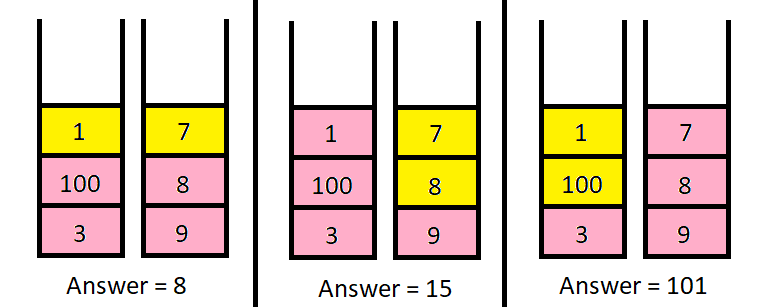
输入:piles = [[1,100,3],[7,8,9]], k = 2
输出:101
解释:
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。
示例 2:
输入:piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
输出:706
解释:
如果我们所有硬币都从最后一个栈中取,可以得到最大面值和。
提示:
n == piles.length1 <= n <= 10001 <= piles[i][j] <= 1051 <= k <= sum(piles[i].length) <= 2000
Metadata
- Link: Maximum Value of K Coins From Piles
- Difficulty: Hard
- Tag:
ArrayDynamic ProgrammingPrefix Sum
There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.
In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.
Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.
Example 1:

Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
Example 2:
Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.
Constraints:
n == piles.length1 <= n <= 10001 <= piles[i][j] <= 1051 <= k <= sum(piles[i].length) <= 2000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maxValueOfCoins(vector<vector<int>> &piles, int k) {
vector<int> f(k + 1, 0);
for (int i = 0; i < piles.size(); i++) {
for (int j = k; j > 0; j--) {
int v = 0;
for (int o = 0; o < piles[i].size(); o++) {
v += piles[i][o];
int w = o + 1;
if (j - w >= 0) {
f[j] = max(f[j], f[j - w] + v);
} else {
break;
}
}
}
}
return f[k];
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif