weekly-contest-295
A
Statement
Metadata
- Link: 重排字符形成目标字符串
- Difficulty: Easy
- Tag:
给你两个下标从 0 开始的字符串 s 和 target 。你可以从 s 取出一些字符并将其重排,得到若干新的字符串。
从 s 中取出字符并重新排列,返回可以形成 target 的 最大 副本数。
示例 1:
输入:s = "ilovecodingonleetcode", target = "code"
输出:2
解释:
对于 "code" 的第 1 个副本,选取下标为 4 、5 、6 和 7 的字符。
对于 "code" 的第 2 个副本,选取下标为 17 、18 、19 和 20 的字符。
形成的字符串分别是 "ecod" 和 "code" ,都可以重排为 "code" 。
可以形成最多 2 个 "code" 的副本,所以返回 2 。
示例 2:
输入:s = "abcba", target = "abc"
输出:1
解释:
选取下标为 0 、1 和 2 的字符,可以形成 "abc" 的 1 个副本。
可以形成最多 1 个 "abc" 的副本,所以返回 1 。
注意,尽管下标 3 和 4 分别有额外的 'a' 和 'b' ,但不能重用下标 2 处的 'c' ,所以无法形成 "abc" 的第 2 个副本。
示例 3:
输入:s = "abbaccaddaeea", target = "aaaaa"
输出:1
解释:
选取下标为 0 、3 、6 、9 和 12 的字符,可以形成 "aaaaa" 的 1 个副本。
可以形成最多 1 个 "aaaaa" 的副本,所以返回 1 。
提示:
1 <= s.length <= 1001 <= target.length <= 10s和target由小写英文字母组成
Metadata
- Link: Rearrange Characters to Make Target String
- Difficulty: Easy
- Tag:
You are given two 0-indexed strings s and target. You can take some letters from s and rearrange them to form new strings.
Return the maximum number of copies of target that can be formed by taking letters from s and rearranging them.
Example 1:
Input: s = "ilovecodingonleetcode", target = "code"
Output: 2
Explanation:
For the first copy of "code", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod" and "code" which can both be rearranged into "code".
We can make at most two copies of "code", so we return 2.
Example 2:
Input: s = "abcba", target = "abc"
Output: 1
Explanation:
We can make one copy of "abc" by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc".
Example 3:
Input: s = "abbaccaddaeea", target = "aaaaa"
Output: 1
Explanation:
We can make one copy of "aaaaa" by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa", so we return 1.
Constraints:
1 <= s.length <= 1001 <= target.length <= 10sandtargetconsist of lowercase English letters.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
// solution class
const int INF = 0x3f3f3f3f;
class Solution {
public:
int rearrangeCharacters(string s, string target) {
vector<char> need(30, 0), has(30, 0);
for (const char &c : target) {
++need[c - 'a'];
}
for (const char &c : s) {
++has[c - 'a'];
}
int res = INF;
for (int i = 0; i < 26; i++) {
if (need[i] == 0) {
continue;
}
if (need[i] > has[i]) {
return 0;
}
res = min(res, has[i] / need[i]);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 价格减免
- Difficulty: Medium
- Tag:
句子 是由若干个单词组成的字符串,单词之间用单个空格分隔,其中每个单词可以包含数字、小写字母、和美元符号 '$' 。如果单词的形式为美元符号后跟着一个非负实数,那么这个单词就表示一个价格。
- 例如
"$100"、"$23"和"$6.75"表示价格,而"100"、"$"和"2$3"不是。
注意:本题输入中的价格均为整数。
给你一个字符串 sentence 和一个整数 discount 。对于每个表示价格的单词,都在价格的基础上减免 discount% ,并 更新 该单词到句子中。所有更新后的价格应该表示为一个 恰好保留小数点后两位 的数字。
返回表示修改后句子的字符串。
示例 1:
输入:sentence = "there are $1 $2 and 5$ candies in the shop", discount = 50
输出:"there are $0.50 $1.00 and 5$ candies in the shop"
解释:
表示价格的单词是 "$1" 和 "$2" 。
- "$1" 减免 50% 为 "$0.50" ,所以 "$1" 替换为 "$0.50" 。
- "$2" 减免 50% 为 "$1" ,所以 "$1" 替换为 "$1.00" 。示例 2:
输入:sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$", discount = 100
输出:"1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$"
解释:
任何价格减免 100% 都会得到 0 。
表示价格的单词分别是 "$3"、"$5"、"$6" 和 "$9"。
每个单词都替换为 "$0.00"。
提示:
1 <= sentence.length <= 105sentence由小写英文字母、数字、' '和'$'组成sentence不含前导和尾随空格sentence的所有单词都用单个空格分隔- 所有价格都是 正 整数且不含前导零
- 所有价格 最多 为
10位数字 0 <= discount <= 100
Metadata
- Link: Apply Discount to Prices
- Difficulty: Medium
- Tag:
A sentence is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign '$'. A word represents a price if it is a non-negative real number preceded by a dollar sign.
- For example,
"$100","$23", and"$6.75"represent prices while"100","$", and"2$3"do not.
You are given a string sentence representing a sentence and an integer discount. For each word representing a price, apply a discount of discount% on the price and update the word in the sentence. All updated prices should be represented with exactly two decimal places.
Return a string representing the modified sentence.
Example 1:
Input: sentence = "there are $1 $2 and 5$ candies in the shop", discount = 50
Output: "there are $0.50 $1.00 and 5$ candies in the shop"
Explanation:
The words which represent prices are "$1" and "$2".
- A 50% discount on "$1" yields "$0.50", so "$1" is replaced by "$0.50".
- A 50% discount on "$2" yields "$1". Since we need to have exactly 2 decimal places after a price, we replace "$2" with "$1.00".
Example 2:
Input: sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$", discount = 100
Output: "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$"
Explanation:
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3", "$5", "$6", and "$9".
Each of them is replaced by "$0.00".
Constraints:
1 <= sentence.length <= 105sentenceconsists of lowercase English letters, digits,' ', and'$'.sentencedoes not have leading or trailing spaces.- All words in
sentenceare separated by a single space. - All prices will be positive integers without leading zeros.
- All prices will have at most
10digits. 0 <= discount <= 100
Solution
from calendar import c
class Solution:
def discountPrices(self, sentence: str, discount: int) -> str:
strl = sentence.split(' ')
for i in range(len(strl)):
if (strl[i][0] != '$'):
continue
try:
a = int(strl[i][1:])
if str(a) == strl[i][1:]:
strl[i] = '$' + ("%.2f" % (a - (a * discount / 100)))
continue
except ValueError:
pass
try:
b = float(strl[i][1:])
if str(b) == strl([i][1:]):
strl[i] = '$' + ("%.2f" % (a - (a * discount / 100)))
except ValueError:
pass
return " ".join(strl)
C
Statement
Metadata
- Link: 使数组按非递减顺序排列
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的整数数组 nums 。在一步操作中,移除所有满足 nums[i - 1] > nums[i] 的 nums[i] ,其中 0 < i < nums.length 。
重复执行步骤,直到 nums 变为 非递减 数组,返回所需执行的操作数。
示例 1:
输入:nums = [5,3,4,4,7,3,6,11,8,5,11]
输出:3
解释:执行下述几个步骤:
- 步骤 1 :[5,3,4,4,7,3,6,11,8,5,11] 变为 [5,4,4,7,6,11,11]
- 步骤 2 :[5,4,4,7,6,11,11] 变为 [5,4,7,11,11]
- 步骤 3 :[5,4,7,11,11] 变为 [5,7,11,11]
[5,7,11,11] 是一个非递减数组,因此,返回 3 。
示例 2:
输入:nums = [4,5,7,7,13]
输出:0
解释:nums 已经是一个非递减数组,因此,返回 0 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
Metadata
- Link: Steps to Make Array Non-decreasing
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array nums. In one step, remove all elements nums[i] where nums[i - 1] > nums[i] for all 0 < i < nums.length.
Return the number of steps performed until nums becomes a non-decreasing array.
Example 1:
Input: nums = [5,3,4,4,7,3,6,11,8,5,11]
Output: 3
Explanation: The following are the steps performed:
- Step 1: [5,3,4,4,7,3,6,11,8,5,11] becomes [5,4,4,7,6,11,11]
- Step 2: [5,4,4,7,6,11,11] becomes [5,4,7,11,11]
- Step 3: [5,4,7,11,11] becomes [5,7,11,11]
[5,7,11,11] is a non-decreasing array. Therefore, we return 3.
Example 2:
Input: nums = [4,5,7,7,13]
Output: 0
Explanation: nums is already a non-decreasing array. Therefore, we return 0.
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 109
Solution
#include <bits/stdc++.h>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int INF = 0x3f3f3f3f;
// 9 8 7 6 5 4 3 2
// 10 9 1 2 3 4 5 6 7 8
// 7 15 4 14 13 2 6 13
// 7 15 14 6 13
// 7 15 13
// 7 15
// 7 14 4 14 13 2 6 13
// 7 14 14 6 13
// 7 14 14 13
// 7 14 14
class Solution {
public:
int totalSteps(vector<int> &a) {
int n = a.size();
vector<int> dp(n, 0);
vector<int> st;
st.push_back(0);
for (int i = 1; i < n; i++) {
int cur = 0;
while (!st.empty() && a[st.back()] <= a[i]) {
cur = max(cur, dp[st.back()]);
st.pop_back();
}
if (!st.empty()) {
dp[i] = cur + 1;
}
st.push_back(i);
}
return *max_element(dp.begin(), dp.end());
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 到达角落需要移除障碍物的最小数目
- Difficulty: Hard
- Tag:
给你一个下标从 0 开始的二维整数数组 grid ,数组大小为 m x n 。每个单元格都是两个值之一:
0表示一个 空 单元格,1表示一个可以移除的 障碍物 。
你可以向上、下、左、右移动,从一个空单元格移动到另一个空单元格。
现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ,返回需要移除的障碍物的 最小 数目。
示例 1:
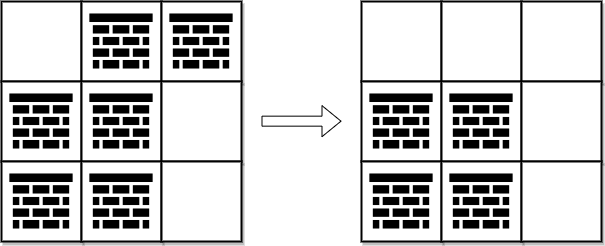
输入:grid = [[0,1,1],[1,1,0],[1,1,0]]
输出:2
解释:可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。
可以证明我们至少需要移除两个障碍物,所以返回 2 。
注意,可能存在其他方式来移除 2 个障碍物,创建出可行的路径。
示例 2:
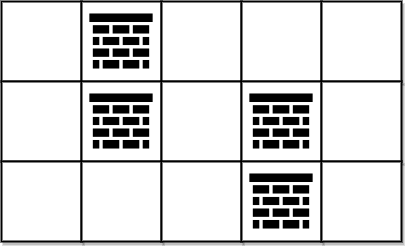
输入:grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
输出:0
解释:不移除任何障碍物就能从 (0, 0) 到 (2, 4) ,所以返回 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1052 <= m * n <= 105grid[i][j]为0或1grid[0][0] == grid[m - 1][n - 1] == 0
Metadata
- Link: Minimum Obstacle Removal to Reach Corner
- Difficulty: Hard
- Tag:
You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:
0represents an empty cell,1represents an obstacle that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).
Example 1:

Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
Output: 2
Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.
Example 2:

Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
Output: 0
Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1052 <= m * n <= 105grid[i][j]is either0or1.grid[0][0] == grid[m - 1][n - 1] == 0
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <queue>
#include <utility>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int INF = 0x3f3f3f3f;
struct node {
int x, y, w;
node(int x, int y, int w) : x(x), y(y), w(w) {}
bool operator<(const node &rhs) const {
return w > rhs.w;
}
};
int mv[][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
class Solution {
public:
int minimumObstacles(vector<vector<int>> &g) {
int n = g.size();
int m = g[0].size();
priority_queue<node> pq;
vector<vector<int>> dp(n + 1, vector<int>(m + 1, INF));
dp[0][0] = g[0][0];
pq.push(node(0, 0, g[0][0]));
while (!pq.empty()) {
node cur = pq.top();
pq.pop();
if (cur.x == n - 1 && cur.y == m - 1) {
return cur.w;
}
for (int i = 0; i < 4; i++) {
int nx = cur.x + mv[i][0];
int ny = cur.y + mv[i][1];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
continue;
}
int nw = cur.w + g[nx][ny];
if (dp[nx][ny] <= nw) {
continue;
}
dp[nx][ny] = nw;
pq.push(node(nx, ny, nw));
}
}
assert(false);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif