跳转至

weekly-contest-212

A

Statement

Metadata

LeetCode 设计了一款新式键盘，正在测试其可用性。测试人员将会点击一系列键（总计 n 个），每次一个。

给你一个长度为 n 的字符串 keysPressed ，其中 keysPressed[i] 表示测试序列中第 i 个被按下的键。releaseTimes 是一个升序排列的列表，其中 releaseTimes[i] 表示松开第 i 个键的时间。字符串和数组的 下标都从 0 开始 。第 0 个键在时间为 0 时被按下，接下来每个键都 恰好 在前一个键松开时被按下。

测试人员想要找出按键 持续时间最长 的键。第 i 次按键的持续时间为 releaseTimes[i] - releaseTimes[i - 1] ，第 0 次按键的持续时间为 releaseTimes[0] 。

注意，测试期间，同一个键可以在不同时刻被多次按下，而每次的持续时间都可能不同。

请返回单次按键 持续时间最长 的键，如果有多个这样的键，则返回 按字母顺序排列最大 的那个键。

 

示例 1：

输入：releaseTimes = [9,29,49,50], keysPressed = "cbcd"
输出："c"
解释：按键顺序和持续时间如下：
按下 'c' ，持续时间 9（时间 0 按下，时间 9 松开）
按下 'b' ，持续时间 29 - 9 = 20（松开上一个键的时间 9 按下，时间 29 松开）
按下 'c' ，持续时间 49 - 29 = 20（松开上一个键的时间 29 按下，时间 49 松开）
按下 'd' ，持续时间 50 - 49 = 1（松开上一个键的时间 49 按下，时间 50 松开）
按键持续时间最长的键是 'b' 和 'c'（第二次按下时），持续时间都是 20
'c' 按字母顺序排列比 'b' 大，所以答案是 'c'

示例 2：

输入：releaseTimes = [12,23,36,46,62], keysPressed = "spuda"
输出："a"
解释：按键顺序和持续时间如下：
按下 's' ，持续时间 12
按下 'p' ，持续时间 23 - 12 = 11
按下 'u' ，持续时间 36 - 23 = 13
按下 'd' ，持续时间 46 - 36 = 10
按下 'a' ，持续时间 62 - 46 = 16
按键持续时间最长的键是 'a' ，持续时间 16

 

提示：

  • releaseTimes.length == n
  • keysPressed.length == n
  • 2 <= n <= 1000
  • 1 <= releaseTimes[i] <= 109
  • releaseTimes[i] < releaseTimes[i+1]
  • keysPressed 仅由小写英文字母组成

Metadata

A newly designed keypad was tested, where a tester pressed a sequence of n keys, one at a time.

You are given a string keysPressed of length n, where keysPressed[i] was the ith key pressed in the testing sequence, and a sorted list releaseTimes, where releaseTimes[i] was the time the ith key was released. Both arrays are 0-indexed. The 0th key was pressed at the time 0, and every subsequent key was pressed at the exact time the previous key was released.

The tester wants to know the key of the keypress that had the longest duration. The ith keypress had a duration of releaseTimes[i] - releaseTimes[i - 1], and the 0th keypress had a duration of releaseTimes[0].

Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key may not have had the same duration.

Return the key of the keypress that had the longest duration. If there are multiple such keypresses, return the lexicographically largest key of the keypresses.

 

Example 1:

Input: releaseTimes = [9,29,49,50], keysPressed = "cbcd"
Output: "c"
Explanation: The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.

Example 2:

Input: releaseTimes = [12,23,36,46,62], keysPressed = "spuda"
Output: "a"
Explanation: The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.

 

Constraints:

  • releaseTimes.length == n
  • keysPressed.length == n
  • 2 <= n <= 1000
  • 1 <= releaseTimes[i] <= 109
  • releaseTimes[i] < releaseTimes[i+1]
  • keysPressed contains only lowercase English letters.

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    char slowestKey(vector<int> &releaseTimes, string keysPressed) {
        n = releaseTimes.size();
        vector<int> vec(220, 0);
        int pre = 0;
        for (int i = 0; i < n; ++i) {
            int t = releaseTimes[i] - pre;
            int ch = keysPressed[i];
            chmax(vec[ch], t);
            pre = releaseTimes[i];
        }
        int Max = 0;
        char ch = 'z';
        for (int i = 'z'; i >= 'a'; --i) {
            if (vec[i] > Max) {
                Max = vec[i];
                ch = i;
            }
        }
        return ch;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

Metadata

如果一个数列由至少两个元素组成，且每两个连续元素之间的差值都相同，那么这个序列就是 等差数列 。更正式地，数列 s 是等差数列，只需要满足：对于每个有效的 i ， s[i+1] - s[i] == s[1] - s[0] 都成立。

例如，下面这些都是 等差数列 ：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的数列 不是等差数列 ：

1, 1, 2, 5, 7

给你一个由 n 个整数组成的数组 nums，和两个由 m 个整数组成的数组 l 和 r，后两个数组表示 m 组范围查询，其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。

返回 boolean 元素构成的答案列表 answer 。如果子数组 nums[l[i]], nums[l[i]+1], … , nums[r[i]] 可以 重新排列 形成 等差数列 ，answer[i] 的值就是 true；否则answer[i] 的值就是 false 。

 

示例 1：

输入：nums = [4,6,5,9,3,7], l = [0,0,2], r = [2,3,5]
输出：[true,false,true]
解释：
第 0 个查询，对应子数组 [4,6,5] 。可以重新排列为等差数列 [6,5,4] 。
第 1 个查询，对应子数组 [4,6,5,9] 。无法重新排列形成等差数列。
第 2 个查询，对应子数组 [5,9,3,7] 。可以重新排列为等差数列 [3,5,7,9] 。

示例 2：

输入：nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10]
输出：[false,true,false,false,true,true]

 

提示：

  • n == nums.length
  • m == l.length
  • m == r.length
  • 2 <= n <= 500
  • 1 <= m <= 500
  • 0 <= l[i] < r[i] < n
  • -105 <= nums[i] <= 105

Metadata

A sequence of numbers is called arithmetic if it consists of at least two elements, and the difference between every two consecutive elements is the same. More formally, a sequence s is arithmetic if and only if s[i+1] - s[i] == s[1] - s[0] for all valid i.

For example, these are arithmetic sequences:

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

The following sequence is not arithmetic:

1, 1, 2, 5, 7

You are given an array of n integers, nums, and two arrays of m integers each, l and r, representing the m range queries, where the ith query is the range [l[i], r[i]]. All the arrays are 0-indexed.

Return a list of boolean elements answer, where answer[i] is true if the subarray nums[l[i]], nums[l[i]+1], … , nums[r[i]] can be rearranged to form an arithmetic sequence, and false otherwise.

 

Example 1:

Input: nums = [4,6,5,9,3,7], l = [0,0,2], r = [2,3,5]
Output: [true,false,true]
Explanation:
In the 0th query, the subarray is [4,6,5]. This can be rearranged as [6,5,4], which is an arithmetic sequence.
In the 1st query, the subarray is [4,6,5,9]. This cannot be rearranged as an arithmetic sequence.
In the 2nd query, the subarray is [5,9,3,7]. This can be rearranged as [3,5,7,9], which is an arithmetic sequence.

Example 2:

Input: nums = [-12,-9,-3,-12,-6,15,20,-25,-20,-15,-10], l = [0,1,6,4,8,7], r = [4,4,9,7,9,10]
Output: [false,true,false,false,true,true]

 

Constraints:

  • n == nums.length
  • m == l.length
  • m == r.length
  • 2 <= n <= 500
  • 1 <= m <= 500
  • 0 <= l[i] < r[i] < n
  • -105 <= nums[i] <= 105

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1& x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1& x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1& x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T& arg, Ts&... args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t>& arg, const A&... args) {
    for (auto& v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T& arg, const Ts&... args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T& arg, const Ts&... args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t>& arg, const A&... args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n, q;

class Solution {
public:
    vector<bool> checkArithmeticSubarrays(vector<int>& nums, vector<int>& l, vector<int>& r) {
        n = nums.size();
        q = l.size();
        vector<bool> res;
        for (int i = 0; i < q; ++i) {
            int _l = l[i], _r = r[i];
            vector<int> vec;
            for (int j = _l; j <= _r; ++j) vec.push_back(nums[j]);
            sort(all(vec));
            if (SZ(vec) == 1)
                res.push_back(true);
            else {
                int gap = vec[1] - vec[0];
                bool ok = true;
                for (int i = 2; i < SZ(vec); ++i) {
                    if (vec[i] - vec[i - 1] != gap) {
                        ok = 0;
                        break;
                    }
                }
                res.push_back(ok);
            }
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

Metadata
  • Link: 最小体力消耗路径
  • Difficulty: Medium
  • Tag: 深度优先搜索 广度优先搜索 并查集 数组 二分查找 矩阵 堆（优先队列）

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

 

示例 1：

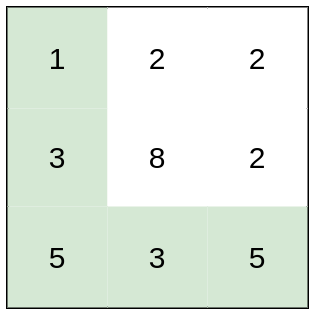
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

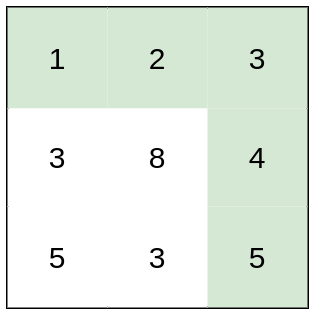
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

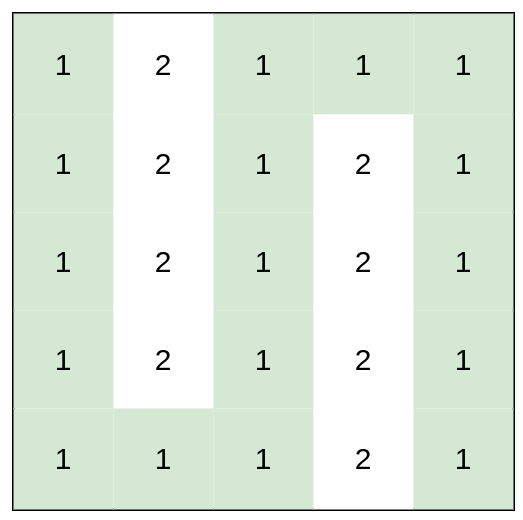
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

 

提示：

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

Metadata
  • Link: Path With Minimum Effort
  • Difficulty: Medium
  • Tag: Depth-First Search Breadth-First Search Union Find Array Binary Search Matrix Heap (Priority Queue)

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:


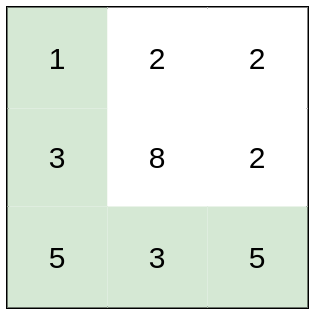
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:


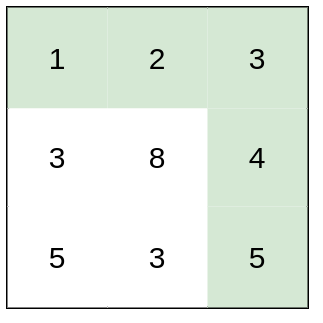
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:


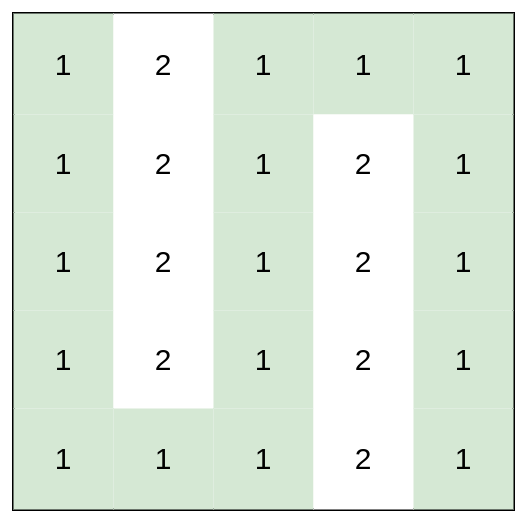
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e2 + 10;
int n, m;
vector<vector<int>> heights;
int vis[N][N];

int Move[][2] = {-1, 0, 1, 0, 0, 1, 0, -1};

bool valid(int x, int y) {
    if (x < 0 || x >= n || y < 0 || y >= m)
        return false;
    return true;
}

bool ok(int xx) {
    memset(vis, 0, sizeof vis);
    queue<pII> que;
    que.push(pII(0, 0));
    while (!que.empty()) {
        pII front = que.front();
        que.pop();
        int x = front.fi;
        int y = front.se;
        if (x == n - 1 && y == m - 1)
            return true;
        for (int i = 0; i < 4; ++i) {
            int _x = x + Move[i][0];
            int _y = y + Move[i][1];
            if (valid(_x, _y) && vis[_x][_y] == 0 && abs(heights[_x][_y] - heights[x][y]) <= xx) {
                que.push(pII(_x, _y));
                vis[_x][_y] = 1;
            }
        }
    }
    return false;
}

class Solution {
public:
    int minimumEffortPath(vector<vector<int>> &_heights) {
        heights = _heights;
        n = heights.size();
        m = heights[0].size();
        int l = 0, r = 1e6, res = 1e6;
        while (r - l >= 0) {
            int mid = (l + r) >> 1;
            if (ok(mid)) {
                res = mid;
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

Metadata

给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

  • 秩是从 1 开始的一个整数。
  • 如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：
    • 如果 p < q ，那么 rank(p) < rank(q)
    • 如果 p == q ，那么 rank(p) == rank(q)
    • 如果 p > q ，那么 rank(p) > rank(q)
  • 秩 需要越 小 越好。

题目保证按照上面规则 answer 数组是唯一的。

 

示例 1：

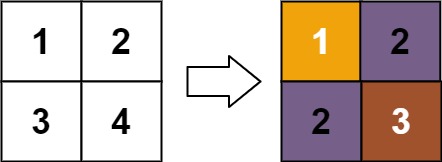
输入：matrix = [[1,2],[3,4]]
输出：[[1,2],[2,3]]
解释：
matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。
matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。

示例 2：

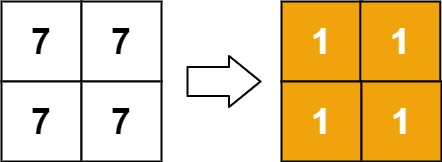
输入：matrix = [[7,7],[7,7]]
输出：[[1,1],[1,1]]

示例 3：

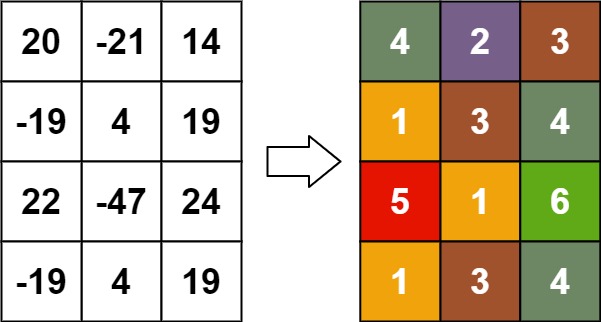
输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

示例 4：

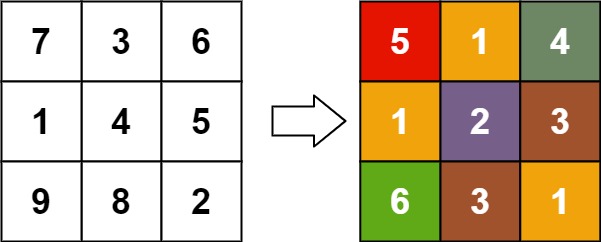
输入：matrix = [[7,3,6],[1,4,5],[9,8,2]]
输出：[[5,1,4],[1,2,3],[6,3,1]]

 

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

Metadata

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

  • The rank is an integer starting from 1.
  • If two elements p and q are in the same row or column, then:
    • If p < q then rank(p) < rank(q)
    • If p == q then rank(p) == rank(q)
    • If p > q then rank(p) > rank(q)
  • The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

 

Example 1:

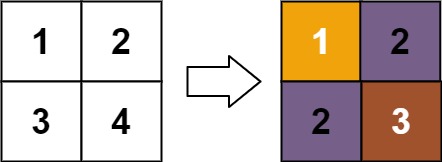
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

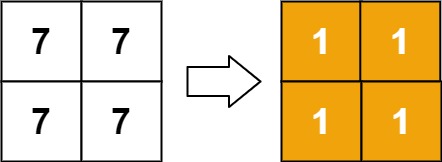
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

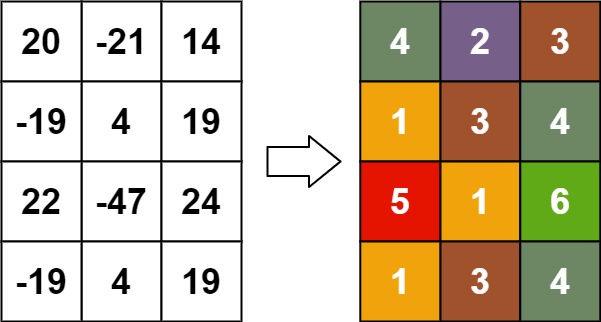
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 500 * 500 + 10;
int n, m, f[N], d[N];
vector<vector<int>> matrix;
vector<vector<int>> G;

int id(int x, int y) {
    return x * m + y;
}

struct UFS {
    int fa[N], rk[N];
    void init(int n) {
        memset(fa, -1, sizeof(fa[0]) * (n + 5));
        memset(rk, 0, sizeof(rk[0]) * (n + 5));
    }
    int find(int x) {
        return fa[x] == -1 ? x : fa[x] = find(fa[x]);
    }
    bool merge(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx != fy) {
            if (rk[fx] > rk[fy])
                swap(fx, fy);
            fa[fx] = fy;
            if (rk[fx] == rk[fy])
                ++rk[fy];
            return true;
        }
        return false;
    }
    bool same(int x, int y) {
        return find(x) == find(y);
    }
} ufs;

void topo() {
    queue<int> que;
    memset(f, 0, sizeof f);
    for (int i = 0; i < n * m; ++i) {
        if (d[i] == 0) {
            f[i] = 1;
            que.push(i);
        }
    }
    while (!que.empty()) {
        int u = que.front();
        que.pop();
        for (auto &v : G[u]) {
            chmax(f[v], f[u] + 1);
            if (--d[v] == 0) {
                que.push(v);
            }
        }
    }
}

class Solution {
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>> &_matrix) {
        matrix = _matrix;
        n = matrix.size();
        m = matrix[0].size();
        G.clear();
        G.resize(N);
        memset(d, 0, sizeof d);
        ufs.init(N - 10);
        for (int i = 0; i < n; ++i) {
            vector<pII> vec;
            for (int j = 0; j < m; ++j) {
                vec.push_back(pII(matrix[i][j], j));
            }
            sort(all(vec));
            for (int j = 1; j < m; ++j) {
                if (vec[j].fi == vec[j - 1].fi) {
                    int u = id(i, vec[j - 1].se);
                    int v = id(i, vec[j].se);
                    ufs.merge(u, v);
                }
            }
        }
        for (int j = 0; j < m; ++j) {
            vector<pII> vec;
            for (int i = 0; i < n; ++i) {
                vec.push_back(pII(matrix[i][j], i));
            }
            sort(all(vec));
            for (int i = 1; i < n; ++i) {
                if (vec[i].fi == vec[i - 1].fi) {
                    int u = id(vec[i - 1].se, j);
                    int v = id(vec[i].se, j);
                    ufs.merge(u, v);
                }
            }
        }
        for (int i = 0; i < n; ++i) {
            vector<pII> vec;
            for (int j = 0; j < m; ++j) {
                vec.push_back(pII(matrix[i][j], j));
            }
            sort(all(vec));
            for (int j = 1; j < m; ++j) {
                if (vec[j].fi != vec[j - 1].fi) {
                    int u = ufs.find(id(i, vec[j - 1].se));
                    int v = ufs.find(id(i, vec[j].se));
                    G[u].push_back(v);
                    ++d[v];
                }
            }
        }
        for (int j = 0; j < m; ++j) {
            vector<pII> vec;
            for (int i = 0; i < n; ++i) {
                vec.push_back(pII(matrix[i][j], i));
            }
            sort(all(vec));
            for (int i = 1; i < n; ++i) {
                if (vec[i].fi != vec[i - 1].fi) {
                    int u = ufs.find(id(vec[i - 1].se, j));
                    int v = ufs.find(id(vec[i].se, j));
                    G[u].push_back(v);
                    ++d[v];
                }
            }
        }
        topo();
        vector<vector<int>> res(n, vector<int>(m));
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < m; ++j) res[i][j] = f[ufs.find(id(i, j))];
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部