biweekly-contest-36
A
Statement
Metadata
- Link: 设计停车系统
- Difficulty: Easy
- Tag:
设计计数模拟
请你给一个停车场设计一个停车系统。停车场总共有三种不同大小的车位:大,中和小,每种尺寸分别有固定数目的车位。
请你实现 ParkingSystem 类:
ParkingSystem(int big, int medium, int small)初始化ParkingSystem类,三个参数分别对应每种停车位的数目。bool addCar(int carType)检查是否有carType对应的停车位。carType有三种类型:大,中,小,分别用数字1,2和3表示。一辆车只能停在carType对应尺寸的停车位中。如果没有空车位,请返回false,否则将该车停入车位并返回true。
示例 1:
输入:
["ParkingSystem", "addCar", "addCar", "addCar", "addCar"]
[[1, 1, 0], [1], [2], [3], [1]]
输出:
[null, true, true, false, false]
解释:
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // 返回 true ,因为有 1 个空的大车位
parkingSystem.addCar(2); // 返回 true ,因为有 1 个空的中车位
parkingSystem.addCar(3); // 返回 false ,因为没有空的小车位
parkingSystem.addCar(1); // 返回 false ,因为没有空的大车位,唯一一个大车位已经被占据了
提示:
0 <= big, medium, small <= 1000carType取值为1,2或3- 最多会调用
addCar函数1000次
Metadata
- Link: Design Parking System
- Difficulty: Easy
- Tag:
DesignCountingSimulation
Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.
Implement the ParkingSystem class:
ParkingSystem(int big, int medium, int small)Initializes object of theParkingSystemclass. The number of slots for each parking space are given as part of the constructor.bool addCar(int carType)Checks whether there is a parking space ofcarTypefor the car that wants to get into the parking lot.carTypecan be of three kinds: big, medium, or small, which are represented by1,2, and3respectively. A car can only park in a parking space of itscarType. If there is no space available, returnfalse, else park the car in that size space and returntrue.
Example 1:
Input
["ParkingSystem", "addCar", "addCar", "addCar", "addCar"]
[[1, 1, 0], [1], [2], [3], [1]]
Output
[null, true, true, false, false]
Explanation
ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0);
parkingSystem.addCar(1); // return true because there is 1 available slot for a big car
parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car
parkingSystem.addCar(3); // return false because there is no available slot for a small car
parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.
Constraints:
0 <= big, medium, small <= 1000carTypeis1,2, or3- At most
1000calls will be made toaddCar
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class ParkingSystem {
public:
int x[4];
ParkingSystem(int big, int medium, int small) {
x[1] = big;
x[2] = medium;
x[3] = small;
}
bool addCar(int carType) {
if (x[carType] <= 0)
return false;
else {
--x[carType];
return true;
}
}
};
/**
* Your ParkingSystem object will be instantiated and called as such:
* ParkingSystem* obj = new ParkingSystem(big, medium, small);
* bool param_1 = obj->addCar(carType);
*/
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 警告一小时内使用相同员工卡大于等于三次的人
- Difficulty: Medium
- Tag:
数组哈希表字符串排序
力扣公司的员工都使用员工卡来开办公室的门。每当一个员工使用一次他的员工卡,安保系统会记录下员工的名字和使用时间。如果一个员工在一小时时间内使用员工卡的次数大于等于三次,这个系统会自动发布一个 警告 。
给你字符串数组 keyName 和 keyTime ,其中 [keyName[i], keyTime[i]] 对应一个人的名字和他在 某一天 内使用员工卡的时间。
使用时间的格式是 24小时制 ,形如 "HH:MM" ,比方说 "23:51" 和 "09:49" 。
请你返回去重后的收到系统警告的员工名字,将它们按 字典序升序 排序后返回。
请注意 "10:00" - "11:00" 视为一个小时时间范围内,而 "23:51" - "00:10" 不被视为一小时内,因为系统记录的是某一天内的使用情况。
示例 1:
输入:keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"]
输出:["daniel"]
解释:"daniel" 在一小时内使用了 3 次员工卡("10:00","10:40","11:00")。
示例 2:
输入:keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"]
输出:["bob"]
解释:"bob" 在一小时内使用了 3 次员工卡("21:00","21:20","21:30")。
示例 3:
输入:keyName = ["john","john","john"], keyTime = ["23:58","23:59","00:01"]
输出:[]
示例 4:
输入:keyName = ["leslie","leslie","leslie","clare","clare","clare","clare"], keyTime = ["13:00","13:20","14:00","18:00","18:51","19:30","19:49"]
输出:["clare","leslie"]
提示:
1 <= keyName.length, keyTime.length <= 105keyName.length == keyTime.lengthkeyTime格式为 "HH:MM" 。- 保证
[keyName[i], keyTime[i]]形成的二元对 互不相同 。 1 <= keyName[i].length <= 10keyName[i]只包含小写英文字母。
Metadata
- Link: Alert Using Same Key-Card Three or More Times in a One Hour Period
- Difficulty: Medium
- Tag:
ArrayHash TableStringSorting
LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an alert if any worker uses the key-card three or more times in a one-hour period.
You are given a list of strings keyName and keyTime where [keyName[i], keyTime[i]] corresponds to a person's name and the time when their key-card was used in a single day.
Access times are given in the 24-hour time format "HH:MM", such as "23:51" and "09:49".
Return a list of unique worker names who received an alert for frequent keycard use. Sort the names in ascending order alphabetically.
Notice that "10:00" - "11:00" is considered to be within a one-hour period, while "22:51" - "23:52" is not considered to be within a one-hour period.
Example 1:
Input: keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"]
Output: ["daniel"]
Explanation: "daniel" used the keycard 3 times in a one-hour period ("10:00","10:40", "11:00").
Example 2:
Input: keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"]
Output: ["bob"]
Explanation: "bob" used the keycard 3 times in a one-hour period ("21:00","21:20", "21:30").
Constraints:
1 <= keyName.length, keyTime.length <= 105keyName.length == keyTime.lengthkeyTime[i]is in the format "HH:MM".[keyName[i], keyTime[i]]is unique.1 <= keyName[i].length <= 10keyName[i] contains only lowercase English letters.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
int toInt(char c) {
return c - '0';
}
int change(string time) {
int res = (toInt(time[0]) * 10 + toInt(time[1])) * 60 + toInt(time[3]) * 10 + toInt(time[4]);
return res;
}
class Solution {
public:
vector<string> alertNames(vector<string> &keyName, vector<string> &keyTime) {
map<string, vector<int>> mp;
n = SZ(keyName);
for (int i = 0; i < n; ++i) {
string name = keyName[i];
string time = keyTime[i];
if (mp.count(name) == 0)
mp[name] = vector<int>();
mp[name].push_back(change(time));
}
vector<string> res;
for (auto &it : mp) {
sort(all(it.se));
int ok = 0;
for (int i = 2; i < SZ(it.se); ++i) {
if (it.se[i] - it.se[i - 2] <= 60) {
ok = 1;
break;
}
}
if (ok)
res.push_back(it.fi);
}
sort(all(res));
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 给定行和列的和求可行矩阵
- Difficulty: Medium
- Tag:
贪心数组矩阵
给你两个非负整数数组 rowSum 和 colSum ,其中 rowSum[i] 是二维矩阵中第 i 行元素的和, colSum[j] 是第 j 列元素的和。换言之你不知道矩阵里的每个元素,但是你知道每一行和每一列的和。
请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵,且该矩阵满足 rowSum 和 colSum 的要求。
请你返回任意一个满足题目要求的二维矩阵,题目保证存在 至少一个 可行矩阵。
示例 1:
输入:rowSum = [3,8], colSum = [4,7]
输出:[[3,0],
[1,7]]
解释:
第 0 行:3 + 0 = 3 == rowSum[0]
第 1 行:1 + 7 = 8 == rowSum[1]
第 0 列:3 + 1 = 4 == colSum[0]
第 1 列:0 + 7 = 7 == colSum[1]
行和列的和都满足题目要求,且所有矩阵元素都是非负的。
另一个可行的矩阵为:[[1,2],
[3,5]]
示例 2:
输入:rowSum = [5,7,10], colSum = [8,6,8]
输出:[[0,5,0],
[6,1,0],
[2,0,8]]
示例 3:
输入:rowSum = [14,9], colSum = [6,9,8]
输出:[[0,9,5],
[6,0,3]]
示例 4:
输入:rowSum = [1,0], colSum = [1]
输出:[[1],
[0]]
示例 5:
输入:rowSum = [0], colSum = [0]
输出:[[0]]
提示:
1 <= rowSum.length, colSum.length <= 5000 <= rowSum[i], colSum[i] <= 108sum(rows) == sum(columns)
Metadata
- Link: Find Valid Matrix Given Row and Column Sums
- Difficulty: Medium
- Tag:
GreedyArrayMatrix
You are given two arrays rowSum and colSum of non-negative integers where rowSum[i] is the sum of the elements in the ith row and colSum[j] is the sum of the elements of the jth column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.
Find any matrix of non-negative integers of size rowSum.length x colSum.length that satisfies the rowSum and colSum requirements.
Return a 2D array representing any matrix that fulfills the requirements. It's guaranteed that at least one matrix that fulfills the requirements exists.
Example 1:
Input: rowSum = [3,8], colSum = [4,7]
Output: [[3,0],
[1,7]]
Explanation:
0th row: 3 + 0 = 3 == rowSum[0]
1st row: 1 + 7 = 8 == rowSum[1]
0th column: 3 + 1 = 4 == colSum[0]
1st column: 0 + 7 = 7 == colSum[1]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: [[1,2],
[3,5]]
Example 2:
Input: rowSum = [5,7,10], colSum = [8,6,8]
Output: [[0,5,0],
[6,1,0],
[2,0,8]]
Constraints:
1 <= rowSum.length, colSum.length <= 5000 <= rowSum[i], colSum[i] <= 108sum(rows) == sum(columns)
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1& x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1& x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1& x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T& arg, Ts&... args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t>& arg, const A&... args) {
for (auto& v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T& arg, const Ts&... args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T& arg, const Ts&... args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t>& arg, const A&... args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n, m;
class Solution {
public:
vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum) {
n = SZ(rowSum);
m = SZ(colSum);
vector<vector<int>> res(n, vector<int>(m, 0));
// vector <int> _rowSum(n, 0);
// vector <int> _colSum(m, 0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
int x = min(rowSum[i], colSum[j]);
res[i][j] = x;
rowSum[i] -= x;
colSum[j] -= x;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 找到处理最多请求的服务器
- Difficulty: Hard
- Tag:
贪心数组有序集合堆(优先队列)
你有 k 个服务器,编号为 0 到 k-1 ,它们可以同时处理多个请求组。每个服务器有无穷的计算能力但是 不能同时处理超过一个请求 。请求分配到服务器的规则如下:
- 第
i(序号从 0 开始)个请求到达。 - 如果所有服务器都已被占据,那么该请求被舍弃(完全不处理)。
- 如果第
(i % k)个服务器空闲,那么对应服务器会处理该请求。 - 否则,将请求安排给下一个空闲的服务器(服务器构成一个环,必要的话可能从第 0 个服务器开始继续找下一个空闲的服务器)。比方说,如果第
i个服务器在忙,那么会查看第(i+1)个服务器,第(i+2)个服务器等等。
给你一个 严格递增 的正整数数组 arrival ,表示第 i 个任务的到达时间,和另一个数组 load ,其中 load[i] 表示第 i 个请求的工作量(也就是服务器完成它所需要的时间)。你的任务是找到 最繁忙的服务器 。最繁忙定义为一个服务器处理的请求数是所有服务器里最多的。
请你返回包含所有 最繁忙服务器 序号的列表,你可以以任意顺序返回这个列表。
示例 1:
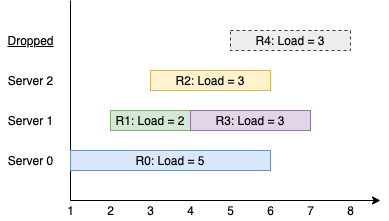
输入:k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3]
输出:[1]
解释:
所有服务器一开始都是空闲的。
前 3 个请求分别由前 3 台服务器依次处理。
请求 3 进来的时候,服务器 0 被占据,所以它呗安排到下一台空闲的服务器,也就是服务器 1 。
请求 4 进来的时候,由于所有服务器都被占据,该请求被舍弃。
服务器 0 和 2 分别都处理了一个请求,服务器 1 处理了两个请求。所以服务器 1 是最忙的服务器。
示例 2:
输入:k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
输出:[0]
解释:
前 3 个请求分别被前 3 个服务器处理。
请求 3 进来,由于服务器 0 空闲,它被服务器 0 处理。
服务器 0 处理了两个请求,服务器 1 和 2 分别处理了一个请求。所以服务器 0 是最忙的服务器。
示例 3:
输入:k = 3, arrival = [1,2,3], load = [10,12,11]
输出:[0,1,2]
解释:每个服务器分别处理了一个请求,所以它们都是最忙的服务器。
示例 4:
输入:k = 3, arrival = [1,2,3,4,8,9,10], load = [5,2,10,3,1,2,2]
输出:[1]
示例 5:
输入:k = 1, arrival = [1], load = [1]
输出:[0]
提示:
1 <= k <= 1051 <= arrival.length, load.length <= 105arrival.length == load.length1 <= arrival[i], load[i] <= 109arrival保证 严格递增 。
Metadata
- Link: Find Servers That Handled Most Number of Requests
- Difficulty: Hard
- Tag:
GreedyArrayOrdered SetHeap (Priority Queue)
You have k servers numbered from 0 to k-1 that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but cannot handle more than one request at a time. The requests are assigned to servers according to a specific algorithm:
- The
ith(0-indexed) request arrives. - If all servers are busy, the request is dropped (not handled at all).
- If the
(i % k)thserver is available, assign the request to that server. - Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the
ithserver is busy, try to assign the request to the(i+1)thserver, then the(i+2)thserver, and so on.
You are given a strictly increasing array arrival of positive integers, where arrival[i] represents the arrival time of the ith request, and another array load, where load[i] represents the load of the ith request (the time it takes to complete). Your goal is to find the busiest server(s). A server is considered busiest if it handled the most number of requests successfully among all the servers.
Return a list containing the IDs (0-indexed) of the busiest server(s). You may return the IDs in any order.
Example 1:
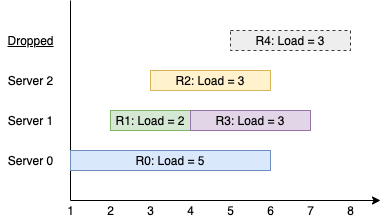
Input: k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3]
Output: [1]
Explanation:
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.
Example 2:
Input: k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
Output: [0]
Explanation:
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.
Example 3:
Input: k = 3, arrival = [1,2,3], load = [10,12,11]
Output: [0,1,2]
Explanation: Each server handles a single request, so they are all considered the busiest.
Constraints:
1 <= k <= 1051 <= arrival.length, load.length <= 105arrival.length == load.length1 <= arrival[i], load[i] <= 109arrivalis strictly increasing.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
using pLI = pair<ll, int>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1& x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1& x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1& x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T& arg, Ts&... args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t>& arg, const A&... args) {
for (auto& v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T& arg, const Ts&... args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T& arg, const Ts&... args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t>& arg, const A&... args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n, f[N];
class Solution {
public:
vector<int> busiestServers(int k, vector<int>& arrival, vector<int>& load) {
vector<int> res;
n = SZ(arrival);
set<int> se;
for (int i = 0; i < k; ++i) {
se.insert(i);
}
memset(f, 0, sizeof f);
priority_queue<pLI, vector<pLI>, greater<pLI>> pq;
for (int i = 0; i < n; ++i) {
ll now = arrival[i];
while (!pq.empty() && pq.top().fi <= now) {
se.insert(pq.top().se);
pq.pop();
}
if (se.empty())
continue;
int x = i % k;
auto pos = se.lower_bound(x);
if (pos == se.end())
pos = se.begin();
++f[*pos];
pq.push(pLI(now + load[i], *pos));
se.erase(pos);
}
int Max = 0;
for (int i = 0; i < k; ++i) {
if (f[i] > Max) {
res.clear();
Max = f[i];
res.push_back(i);
} else if (f[i] == Max) {
res.push_back(i);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif