weekly-contest-312
A
Statement
Metadata
- Link: 按身高排序
- Difficulty: Easy
- Tag:
给你一个字符串数组 names ,和一个由 互不相同 的正整数组成的数组 heights 。两个数组的长度均为 n 。
对于每个下标 i,names[i] 和 heights[i] 表示第 i 个人的名字和身高。
请按身高 降序 顺序返回对应的名字数组 names 。
示例 1:
输入:names = ["Mary","John","Emma"], heights = [180,165,170]
输出:["Mary","Emma","John"]
解释:Mary 最高,接着是 Emma 和 John 。
示例 2:
输入:names = ["Alice","Bob","Bob"], heights = [155,185,150]
输出:["Bob","Alice","Bob"]
解释:第一个 Bob 最高,然后是 Alice 和第二个 Bob 。
提示:
n == names.length == heights.length1 <= n <= 1031 <= names[i].length <= 201 <= heights[i] <= 105names[i]由大小写英文字母组成heights中的所有值互不相同
Metadata
- Link: Sort the People
- Difficulty: Easy
- Tag:
You are given an array of strings names, and an array heights that consists of distinct positive integers. Both arrays are of length n.
For each index i, names[i] and heights[i] denote the name and height of the ith person.
Return names sorted in descending order by the people's heights.
Example 1:
Input: names = ["Mary","John","Emma"], heights = [180,165,170]
Output: ["Mary","Emma","John"]
Explanation: Mary is the tallest, followed by Emma and John.
Example 2:
Input: names = ["Alice","Bob","Bob"], heights = [155,185,150]
Output: ["Bob","Alice","Bob"]
Explanation: The first Bob is the tallest, followed by Alice and the second Bob.
Constraints:
n == names.length == heights.length1 <= n <= 1031 <= names[i].length <= 201 <= heights[i] <= 105names[i]consists of lower and upper case English letters.- All the values of
heightsare distinct.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<string> sortPeople(vector<string> &names, vector<int> &heights) {
int n = int(names.size());
auto vec = vector<pair<int, string>>();
for (int i = 0; i < n; i++) {
vec.push_back(make_pair(heights[i], names[i]));
}
sort(all(vec));
reverse(all(vec));
auto res = vector<string>();
for (int i = 0; i < n; i++) {
res.push_back(vec[i].second);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 按位与最大的最长子数组
- Difficulty: Medium
- Tag:
给你一个长度为 n 的整数数组 nums 。
考虑 nums 中进行 按位与(bitwise AND)运算得到的值 最大 的 非空 子数组。
- 换句话说,令
k是nums任意 子数组执行按位与运算所能得到的最大值。那么,只需要考虑那些执行一次按位与运算后等于k的子数组。
返回满足要求的 最长 子数组的长度。
数组的按位与就是对数组中的所有数字进行按位与运算。
子数组 是数组中的一个连续元素序列。
示例 1:
输入:nums = [1,2,3,3,2,2]
输出:2
解释:
子数组按位与运算的最大值是 3 。
能得到此结果的最长子数组是 [3,3],所以返回 2 。
示例 2:
输入:nums = [1,2,3,4]
输出:1
解释:
子数组按位与运算的最大值是 4 。
能得到此结果的最长子数组是 [4],所以返回 1 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 106
Metadata
- Link: Longest Subarray With Maximum Bitwise AND
- Difficulty: Medium
- Tag:
You are given an integer array nums of size n.
Consider a non-empty subarray from nums that has the maximum possible bitwise AND.
- In other words, let
kbe the maximum value of the bitwise AND of any subarray ofnums. Then, only subarrays with a bitwise AND equal tokshould be considered.
Return the length of the longest such subarray.
The bitwise AND of an array is the bitwise AND of all the numbers in it.
A subarray is a contiguous sequence of elements within an array.
Example 1:
Input: nums = [1,2,3,3,2,2]
Output: 2
Explanation:
The maximum possible bitwise AND of a subarray is 3.
The longest subarray with that value is [3,3], so we return 2.
Example 2:
Input: nums = [1,2,3,4]
Output: 1
Explanation:
The maximum possible bitwise AND of a subarray is 4.
The longest subarray with that value is [4], so we return 1.
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 106
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int longestSubarray(vector<int> &nums) {
int mx = *max_element(all(nums));
int cur = 0;
int res = 0;
for (const auto &a : nums) {
if (a == mx) {
++cur;
} else {
cur = 0;
}
res = max(res, cur);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 找到所有好下标
- Difficulty: Medium
- Tag:
给你一个大小为 n 下标从 0 开始的整数数组 nums 和一个正整数 k 。
对于 k <= i < n - k 之间的一个下标 i ,如果它满足以下条件,我们就称它为一个 好 下标:
- 下标
i之前 的k个元素是 非递增的 。 - 下标
i之后 的k个元素是 非递减的 。
按 升序 返回所有好下标。
示例 1:
输入:nums = [2,1,1,1,3,4,1], k = 2
输出:[2,3]
解释:数组中有两个好下标:
- 下标 2 。子数组 [2,1] 是非递增的,子数组 [1,3] 是非递减的。
- 下标 3 。子数组 [1,1] 是非递增的,子数组 [3,4] 是非递减的。
注意,下标 4 不是好下标,因为 [4,1] 不是非递减的。示例 2:
输入:nums = [2,1,1,2], k = 2
输出:[]
解释:数组中没有好下标。
提示:
n == nums.length3 <= n <= 1051 <= nums[i] <= 1061 <= k <= n / 2
Metadata
- Link: Find All Good Indices
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array nums of size n and a positive integer k.
We call an index i in the range k <= i < n - k good if the following conditions are satisfied:
- The
kelements that are just before the indexiare in non-increasing order. - The
kelements that are just after the indexiare in non-decreasing order.
Return an array of all good indices sorted in increasing order.
Example 1:
Input: nums = [2,1,1,1,3,4,1], k = 2
Output: [2,3]
Explanation: There are two good indices in the array:
- Index 2. The subarray [2,1] is in non-increasing order, and the subarray [1,3] is in non-decreasing order.
- Index 3. The subarray [1,1] is in non-increasing order, and the subarray [3,4] is in non-decreasing order.
Note that the index 4 is not good because [4,1] is not non-decreasing.Example 2:
Input: nums = [2,1,1,2], k = 2
Output: []
Explanation: There are no good indices in this array.
Constraints:
n == nums.length3 <= n <= 1051 <= nums[i] <= 1061 <= k <= n / 2
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> goodIndices(vector<int> &nums, int k) {
int n = int(nums.size());
auto pre = vector<int>(n + 5, 1);
auto suffix = vector<int>(n + 5, 1);
for (int i = 1; i < n; i++) {
if (nums[i] <= nums[i - 1]) {
pre[i] = pre[i - 1] + 1;
}
}
for (int i = n - 2; i >= 0; i--) {
if (nums[i] <= nums[i + 1]) {
suffix[i] = suffix[i + 1] + 1;
}
}
auto res = vector<int>();
for (int i = 1; i < n - 1; i++) {
// cout << i << " " << pre[i - 1] << " " << suffix[i + 1] << endl;
if (pre[i - 1] >= k && suffix[i + 1] >= k) {
res.push_back(i);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 好路径的数目
- Difficulty: Hard
- Tag:
给你一棵 n 个节点的树(连通无向无环的图),节点编号从 0 到 n - 1 且恰好有 n - 1 条边。
给你一个长度为 n 下标从 0 开始的整数数组 vals ,分别表示每个节点的值。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
一条 好路径 需要满足以下条件:
- 开始节点和结束节点的值 相同 。
- 开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值(也就是说开始节点的值应该是路径上所有节点的最大值)。
请你返回不同好路径的数目。
注意,一条路径和它反向的路径算作 同一 路径。比方说, 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。
示例 1:
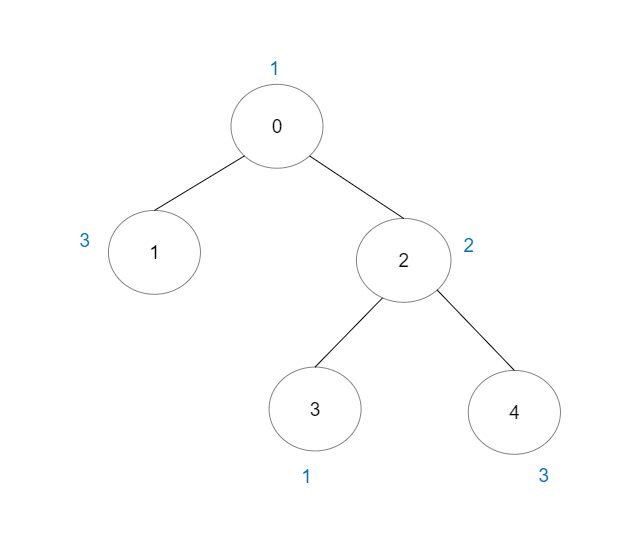
输入:vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
输出:6
解释:总共有 5 条单个节点的好路径。
还有 1 条好路径:1 -> 0 -> 2 -> 4 。
(反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径)
注意 0 -> 2 -> 3 不是一条好路径,因为 vals[2] > vals[0] 。
示例 2:
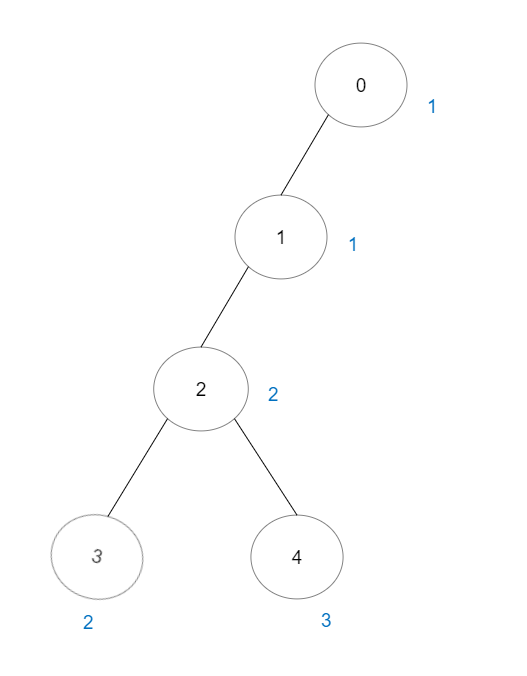
输入:vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
输出:7
解释:总共有 5 条单个节点的好路径。
还有 2 条好路径:0 -> 1 和 2 -> 3 。
示例 3:
输入:vals = [1], edges = []
输出:1
解释:这棵树只有一个节点,所以只有一条好路径。
提示:
n == vals.length1 <= n <= 3 * 1040 <= vals[i] <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵合法的树。
Metadata
- Link: Number of Good Paths
- Difficulty: Hard
- Tag:
There is a tree (i.e. a connected, undirected graph with no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges.
You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the ith node. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.
A good path is a simple path that satisfies the following conditions:
- The starting node and the ending node have the same value.
- All nodes between the starting node and the ending node have values less than or equal to the starting node (i.e. the starting node's value should be the maximum value along the path).
Return the number of distinct good paths.
Note that a path and its reverse are counted as the same path. For example, 0 -> 1 is considered to be the same as 1 -> 0. A single node is also considered as a valid path.
Example 1:

Input: vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
Output: 6
Explanation: There are 5 good paths consisting of a single node.
There is 1 additional good path: 1 -> 0 -> 2 -> 4.
(The reverse path 4 -> 2 -> 0 -> 1 is treated as the same as 1 -> 0 -> 2 -> 4.)
Note that 0 -> 2 -> 3 is not a good path because vals[2] > vals[0].
Example 2:

Input: vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
Output: 7
Explanation: There are 5 good paths consisting of a single node.
There are 2 additional good paths: 0 -> 1 and 2 -> 3.
Example 3:

Input: vals = [1], edges = []
Output: 1
Explanation: The tree consists of only one node, so there is one good path.
Constraints:
n == vals.length1 <= n <= 3 * 1040 <= vals[i] <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 3e4 + 10;
struct UFS {
int fa[N];
unordered_map<int, int> mp[N];
void init(int n) {
for (int i = 0; i <= n; i++) {
fa[i] = 0;
mp[i].clear();
}
}
int find(int x) {
return fa[x] == 0 ? x : fa[x] = find(fa[x]);
}
bool merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx != fy) {
fa[fx] = fy;
for (const auto &[k, v] : mp[fx]) {
mp[fy][k] += v;
}
return true;
}
return false;
}
} ufs;
class Solution {
public:
int numberOfGoodPaths(vector<int> &vals, vector<vector<int>> &edges) {
int n = int(vals.size());
ufs.init(n);
auto node = vector<pair<int, int>>();
for (int i = 0; i < n; i++) {
node.push_back(make_pair(vals[i], i + 1));
}
auto graph = vector<vector<int>>(n + 5, vector<int>());
for (const auto &e : edges) {
graph[e[0] + 1].push_back(e[1] + 1);
graph[e[1] + 1].push_back(e[0] + 1);
}
auto ok_node = vector<int>(n + 1, 0);
int res = 0;
sort(all(node));
for (int i = 0; i < n; i++) {
int _val = node[i].first;
int r = i;
for (int j = i; j < n; j++) {
int val = node[j].first;
if (val != _val) {
break;
}
int u = node[j].second;
r = j;
ok_node[u] = 1;
ufs.mp[u][val] = 1;
for (const auto &v : graph[u]) {
if (ok_node[v]) {
ufs.merge(u, v);
}
}
}
for (int j = i; j <= r; j++) {
int val = node[j].first;
int u = node[j].second;
int rt = ufs.find(u);
auto &mp = ufs.mp[rt];
int tot = mp[val];
res += tot;
}
i = r;
}
res -= (res - n) / 2;
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif