biweekly-contest-38

A

Statement

简体中文English

Metadata

Link: 按照频率将数组升序排序
Difficulty: Easy
Tag: 数组 哈希表 排序

给你一个整数数组 nums ，请你将数组按照每个值的频率升序排序。如果有多个值的频率相同，请你按照数值本身将它们降序排序。

请你返回排序后的数组。

示例 1：

输入：nums = [1,1,2,2,2,3]
输出：[3,1,1,2,2,2]
解释：'3' 频率为 1，'1' 频率为 2，'2' 频率为 3 。

示例 2：

输入：nums = [2,3,1,3,2]
输出：[1,3,3,2,2]
解释：'2' 和 '3' 频率都为 2 ，所以它们之间按照数值本身降序排序。

示例 3：

输入：nums = [-1,1,-6,4,5,-6,1,4,1]
输出：[5,-1,4,4,-6,-6,1,1,1]

提示：

1 <= nums.length <= 100
-100 <= nums[i] <= 100

Metadata

Link: Sort Array by Increasing Frequency
Difficulty: Easy
Tag: Array Hash Table Sorting

Given an array of integers nums, sort the array in increasing order based on the frequency of the values. If multiple values have the same frequency, sort them in decreasing order.

Return the sorted array.

Example 1:

Input: nums = [1,1,2,2,2,3]
Output: [3,1,1,2,2,2]
Explanation: '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.

Example 2:

Input: nums = [2,3,1,3,2]
Output: [1,3,3,2,2]
Explanation: '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.

Example 3:

Input: nums = [-1,1,-6,4,5,-6,1,4,1]
Output: [5,-1,4,4,-6,-6,1,1,1]

Constraints:

1 <= nums.length <= 100
-100 <= nums[i] <= 100

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    vector<int> frequencySort(vector<int> &nums) {
        map<int, int> mp;
        for (auto &it : nums) mp[it] += 1;
        sort(all(nums), [&](int a, int b) {
            if (mp[a] != mp[b])
                return mp[a] < mp[b];
            return a > b;
        });
        return nums;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 两点之间不包含任何点的最宽垂直面积
Difficulty: Medium
Tag: 数组 排序

给你 n 个二维平面上的点 points ，其中 points[i] = [x_i, y_i] ，请你返回两点之间内部不包含任何点的 最宽垂直面积 的宽度。

垂直面积 的定义是固定宽度，而 y 轴上无限延伸的一块区域（也就是高度为无穷大）。 最宽垂直面积 为宽度最大的一个垂直面积。

请注意，垂直区域边上的点不在区域内。

示例 1：

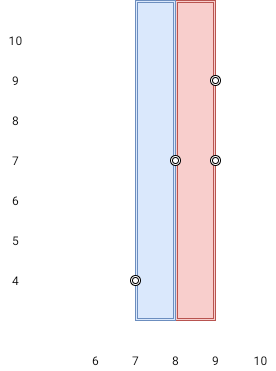
输入：points = [[8,7],[9,9],[7,4],[9,7]]
输出：1
解释：红色区域和蓝色区域都是最优区域。

示例 2：

输入：points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
输出：3

提示：

n == points.length
2 <= n <= 10⁵
points[i].length == 2
0 <= x_i, y_i <= 10⁹

Metadata

Link: Widest Vertical Area Between Two Points Containing No Points
Difficulty: Medium
Tag: Array Sorting

Given n points on a 2D plane where points[i] = [x_i, y_i], Return the widest vertical area between two points such that no points are inside the area.

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Example 1:

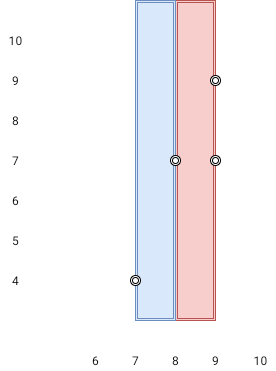
Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

Constraints:

n == points.length
2 <= n <= 10⁵
points[i].length == 2
0 <= x_i, y_i <= 10⁹

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    int maxWidthOfVerticalArea(vector<vector<int>> &points) {
        n = SZ(points);
        sort(all(points), [&](vector<int> a, vector<int> b) {
            return a[0] < b[0];
        });
        int res = 0;
        for (int i = 1; i < n; ++i) chmax(res, points[i][0] - points[i - 1][0]);
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 统计只差一个字符的子串数目
Difficulty: Medium
Tag: 哈希表 字符串 动态规划

给你两个字符串 s 和 t ，请你找出 s 中的非空子串的数目，这些子串满足替换 一个不同字符 以后，是 t 串的子串。换言之，请你找到 s 和 t 串中恰好只有一个字符不同的子字符串对的数目。

比方说， "computer" 和 "computation" 加粗部分只有一个字符不同： 'e'/'a' ，所以这一对子字符串会给答案加 1 。

请你返回满足上述条件的不同子字符串对数目。

一个 子字符串 是一个字符串中连续的字符。

示例 1：

输入：s = "aba", t = "baba"
输出：6
解释：以下为只相差 1 个字符的 s 和 t 串的子字符串对：
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
加粗部分分别表示 s 和 t 串选出来的子字符串。

示例 2：

输入：s = "ab", t = "bb"
输出：3
解释：以下为只相差 1 个字符的 s 和 t 串的子字符串对：
("ab", "bb")
("ab", "bb")
("ab", "bb")
加粗部分分别表示 s 和 t 串选出来的子字符串。

示例 3：

输入：s = "a", t = "a"
输出：0

示例 4：

输入：s = "abe", t = "bbc"
输出：10

提示：

1 <= s.length, t.length <= 100
s 和 t 都只包含小写英文字母。

Metadata

Link: Count Substrings That Differ by One Character
Difficulty: Medium
Tag: Hash Table String Dynamic Programming

Given two strings s and t, find the number of ways you can choose a non-empty substring of s and replace a single character by a different character such that the resulting substring is a substring of t. In other words, find the number of substrings in s that differ from some substring in t by exactly one character.

For example, the underlined substrings in "computer" and "computation" only differ by the 'e'/'a', so this is a valid way.

Return the number of substrings that satisfy the condition above.

A substring is a contiguous sequence of characters within a string.

Example 1:

Input: s = "aba", t = "baba"
Output: 6
Explanation: The following are the pairs of substrings from s and t that differ by exactly 1 character:
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
("aba", "baba")
The underlined portions are the substrings that are chosen from s and t.

Example 2:

Input: s = "ab", t = "bb"
Output: 3
Explanation: The following are the pairs of substrings from s and t that differ by 1 character:
("ab", "bb")
("ab", "bb")
("ab", "bb")
The underlined portions are the substrings that are chosen from s and t.

Constraints:

1 <= s.length, t.length <= 100
s and t consist of lowercase English letters only.

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n, m;

int ok(string s, string t) {
    int len = SZ(t);
    int lens = SZ(s);
    int res = 0;
    for (int i = 0; i + lens <= len; ++i) {
        int l = i, r = i + lens - 1;
        int diff = 0;
        for (int j = l, _i = 0; j <= r; ++j, ++_i) {
            diff += t[j] != s[_i];
        }
        if (diff == 1)
            ++res;
    }
    return res;
}

class Solution {
public:
    int countSubstrings(string s, string t) {
        n = SZ(s);
        m = SZ(t);
        int res = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = i; j < n; ++j) {
                string _s = s.substr(i, j - i + 1);
                res += ok(_s, t);
            }
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 通过给定词典构造目标字符串的方案数
Difficulty: Hard
Tag: 数组 字符串 动态规划

给你一个字符串列表 words 和一个目标字符串 target 。words 中所有字符串都 长度相同 。

你的目标是使用给定的 words 字符串列表按照下述规则构造 target ：

从左到右依次构造 target 的每一个字符。
为了得到 target 第 i 个字符（下标从 0 开始），当 target[i] = words[j][k] 时，你可以使用 words 列表中第 j 个字符串的第 k 个字符。
一旦你使用了 words 中第 j 个字符串的第 k 个字符，你不能再使用 words 字符串列表中任意单词的第 x 个字符（x <= k）。也就是说，所有单词下标小于等于 k 的字符都不能再被使用。
请你重复此过程直到得到目标字符串 target 。

请注意，在构造目标字符串的过程中，你可以按照上述规定使用 words 列表中 同一个字符串 的 多个字符 。

请你返回使用 words 构造 target 的方案数。由于答案可能会很大，请对 10⁹ + 7 取余后返回。

（译者注：此题目求的是有多少个不同的 k 序列，详情请见示例。）

示例 1：

输入：words = ["acca","bbbb","caca"], target = "aba"
输出：6
解释：总共有 6 种方法构造目标串。
"aba" -> 下标为 0 ("acca")，下标为 1 ("bbbb")，下标为 3 ("caca")
"aba" -> 下标为 0 ("acca")，下标为 2 ("bbbb")，下标为 3 ("caca")
"aba" -> 下标为 0 ("acca")，下标为 1 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 0 ("acca")，下标为 2 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 1 ("caca")，下标为 2 ("bbbb")，下标为 3 ("acca")
"aba" -> 下标为 1 ("caca")，下标为 2 ("bbbb")，下标为 3 ("caca")

示例 2：

输入：words = ["abba","baab"], target = "bab"
输出：4
解释：总共有 4 种不同形成 target 的方法。
"bab" -> 下标为 0 ("baab")，下标为 1 ("baab")，下标为 2 ("abba")
"bab" -> 下标为 0 ("baab")，下标为 1 ("baab")，下标为 3 ("baab")
"bab" -> 下标为 0 ("baab")，下标为 2 ("baab")，下标为 3 ("baab")
"bab" -> 下标为 1 ("abba")，下标为 2 ("baab")，下标为 3 ("baab")

示例 3：

输入：words = ["abcd"], target = "abcd"
输出：1

示例 4：

输入：words = ["abab","baba","abba","baab"], target = "abba"
输出：16

提示：

1 <= words.length <= 1000
1 <= words[i].length <= 1000
words 中所有单词长度相同。
1 <= target.length <= 1000
words[i] 和 target 都仅包含小写英文字母。

Metadata

Link: Number of Ways to Form a Target String Given a Dictionary
Difficulty: Hard
Tag: Array String Dynamic Programming

You are given a list of strings of the same length words and a string target.

Your task is to form target using the given words under the following rules:

target should be formed from left to right.
To form the i^th character (0-indexed) of target, you can choose the k^th character of the j^th string in words if target[i] = words[j][k].
Once you use the k^th character of the j^th string of words, you can no longer use the x^th character of any string in words where x <= k. In other words, all characters to the left of or at index k become unusuable for every string.
Repeat the process until you form the string target.

Notice that you can use multiple characters from the same string in words provided the conditions above are met.

Return the number of ways to form target from words. Since the answer may be too large, return it modulo 10⁹ + 7.

Example 1:

Input: words = ["acca","bbbb","caca"], target = "aba"
Output: 6
Explanation: There are 6 ways to form target.
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("caca")
"aba" -> index 0 ("acca"), index 1 ("bbbb"), index 3 ("acca")
"aba" -> index 0 ("acca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("acca")
"aba" -> index 1 ("caca"), index 2 ("bbbb"), index 3 ("caca")

Example 2:

Input: words = ["abba","baab"], target = "bab"
Output: 4
Explanation: There are 4 ways to form target.
"bab" -> index 0 ("baab"), index 1 ("baab"), index 2 ("abba")
"bab" -> index 0 ("baab"), index 1 ("baab"), index 3 ("baab")
"bab" -> index 0 ("baab"), index 2 ("baab"), index 3 ("baab")
"bab" -> index 1 ("abba"), index 2 ("baab"), index 3 ("baab")

Constraints:

1 <= words.length <= 1000
1 <= words[i].length <= 1000
All strings in words have the same length.
1 <= target.length <= 1000
words[i] and target contain only lowercase English letters.

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e3 + 10;
int n, f[N][30];
ll g[N][N];

class Solution {
public:
    int numWays(vector<string> &words, string target) {
        int len = SZ(words[0]);
        memset(f, 0, sizeof f);
        memset(g, 0, sizeof g);
        for (auto &w : words) {
            for (int i = 0; i < len; ++i) {
                ++f[i + 1][w[i] - 'a'];
            }
        }
        int lent = SZ(target);
        for (int i = 0; i <= len; ++i) g[0][i] = 1;
        for (int i = 1; i <= lent; ++i) {
            for (int j = 1; j <= len; ++j) {
                g[i][j] = g[i][j - 1];
                chadd(g[i][j], g[i - 1][j - 1] * f[j][target[i - 1] - 'a'] % mod);
            }
        }
        return g[lent][len];
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023