biweekly-contest-34
A
Statement
Metadata
- Link: 矩阵对角线元素的和
- Difficulty: Easy
- Tag:
数组矩阵
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
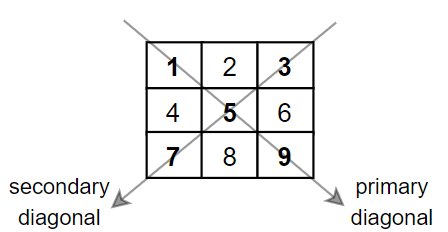
输入:mat = [[1,2,3],
[4,5,6],
[7,8,9]]
输出:25
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25
请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
输出:8
示例 3:
输入:mat = [[5]]
输出:5
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
Metadata
- Link: Matrix Diagonal Sum
- Difficulty: Easy
- Tag:
ArrayMatrix
Given a square matrix mat, return the sum of the matrix diagonals.
Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
Example 1:

Input: mat = [[1,2,3],
[4,5,6],
[7,8,9]]
Output: 25
Explanation: Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat[1][1] = 5 is counted only once.
Example 2:
Input: mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
Output: 8
Example 3:
Input: mat = [[5]]
Output: 5
Constraints:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
int diagonalSum(vector<vector<int>> &mat) {
int n = SZ(mat);
int res = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i - j == 0 || i + j == n - 1) {
res += mat[i][j];
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 分割字符串的方案数
- Difficulty: Medium
- Tag:
数学字符串
给你一个二进制串 s (一个只包含 0 和 1 的字符串),我们可以将 s 分割成 3 个 非空 字符串 s1, s2, s3 (s1 + s2 + s3 = s)。
请你返回分割 s 的方案数,满足 s1,s2 和 s3 中字符 '1' 的数目相同。
由于答案可能很大,请将它对 10^9 + 7 取余后返回。
示例 1:
输入:s = "10101"
输出:4
解释:总共有 4 种方法将 s 分割成含有 '1' 数目相同的三个子字符串。
"1|010|1"
"1|01|01"
"10|10|1"
"10|1|01"
示例 2:
输入:s = "1001"
输出:0
示例 3:
输入:s = "0000"
输出:3
解释:总共有 3 种分割 s 的方法。
"0|0|00"
"0|00|0"
"00|0|0"
示例 4:
输入:s = "100100010100110"
输出:12
提示:
s[i] == '0'或者s[i] == '1'3 <= s.length <= 10^5
Metadata
- Link: Number of Ways to Split a String
- Difficulty: Medium
- Tag:
MathString
Given a binary string s, you can split s into 3 non-empty strings s1, s2, and s3 where s1 + s2 + s3 = s.
Return the number of ways s can be split such that the number of ones is the same in s1, s2, and s3. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
Input: s = "10101"
Output: 4
Explanation: There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1"
"1|01|01"
"10|10|1"
"10|1|01"
Example 2:
Input: s = "1001"
Output: 0
Example 3:
Input: s = "0000"
Output: 3
Explanation: There are three ways to split s in 3 parts.
"0|0|00"
"0|00|0"
"00|0|0"
Constraints:
3 <= s.length <= 105s[i]is either'0'or'1'.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
int numWays(string s) {
n = SZ(s);
int res = 0;
int cnt = 0;
for (auto &ch : s) cnt += (ch - '0');
if (cnt % 3)
return res;
if (cnt == 0) {
ll res = 1ll * (n - 1) * (n - 2) / 2;
res %= mod;
return res;
}
ll x = 0, y = 0;
int num = 0, tar = cnt / 3;
for (int i = 0; i < SZ(s); ++i) {
num += (s[i] - '0');
if (num > tar)
break;
x += num == tar;
}
num = 0;
for (int i = SZ(s) - 1; i >= 0; --i) {
num += (s[i] - '0');
if (num > tar)
break;
y += num == tar;
}
return x * y % mod;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 删除最短的子数组使剩余数组有序
- Difficulty: Medium
- Tag:
栈数组双指针二分查找单调栈
给你一个整数数组 arr ,请你删除一个子数组(可以为空),使得 arr 中剩下的元素是 非递减 的。
一个子数组指的是原数组中连续的一个子序列。
请你返回满足题目要求的最短子数组的长度。
示例 1:
输入:arr = [1,2,3,10,4,2,3,5]
输出:3
解释:我们需要删除的最短子数组是 [10,4,2] ,长度为 3 。剩余元素形成非递减数组 [1,2,3,3,5] 。
另一个正确的解为删除子数组 [3,10,4] 。示例 2:
输入:arr = [5,4,3,2,1]
输出:4
解释:由于数组是严格递减的,我们只能保留一个元素。所以我们需要删除长度为 4 的子数组,要么删除 [5,4,3,2],要么删除 [4,3,2,1]。
示例 3:
输入:arr = [1,2,3]
输出:0
解释:数组已经是非递减的了,我们不需要删除任何元素。
示例 4:
输入:arr = [1]
输出:0
提示:
1 <= arr.length <= 10^50 <= arr[i] <= 10^9
Metadata
- Link: Shortest Subarray to be Removed to Make Array Sorted
- Difficulty: Medium
- Tag:
StackArrayTwo PointersBinary SearchMonotonic Stack
Given an integer array arr, remove a subarray (can be empty) from arr such that the remaining elements in arr are non-decreasing.
Return the length of the shortest subarray to remove.
A subarray is a contiguous subsequence of the array.
Example 1:
Input: arr = [1,2,3,10,4,2,3,5]
Output: 3
Explanation: The shortest subarray we can remove is [10,4,2] of length 3. The remaining elements after that will be [1,2,3,3,5] which are sorted.
Another correct solution is to remove the subarray [3,10,4].
Example 2:
Input: arr = [5,4,3,2,1]
Output: 4
Explanation: Since the array is strictly decreasing, we can only keep a single element. Therefore we need to remove a subarray of length 4, either [5,4,3,2] or [4,3,2,1].
Example 3:
Input: arr = [1,2,3]
Output: 0
Explanation: The array is already non-decreasing. We do not need to remove any elements.
Constraints:
1 <= arr.length <= 1050 <= arr[i] <= 109
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
int findLengthOfShortestSubarray(vector<int> &arr) {
n = SZ(arr);
int l = 0, r = n - 1;
for (int i = 1; i < n; ++i) {
if (arr[i] >= arr[i - 1]) {
l = i;
} else {
break;
}
}
for (int i = n - 2; i >= 0; --i) {
if (arr[i] <= arr[i + 1]) {
r = i;
} else {
break;
}
}
if (l == n - 1)
return 0;
int res = max(l + 1, n - 1 - r + 1);
for (int i = 0; i <= l; ++i) {
while (r <= n - 1 && arr[r] < arr[i]) ++r;
if (r > n - 1)
break;
chmax(res, i + 1 + n - 1 - r + 1);
}
return n - res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 统计所有可行路径
- Difficulty: Hard
- Tag:
记忆化搜索数组动态规划
给你一个 互不相同 的整数数组,其中 locations[i] 表示第 i 个城市的位置。同时给你 start,finish 和 fuel 分别表示出发城市、目的地城市和你初始拥有的汽油总量
每一步中,如果你在城市 i ,你可以选择任意一个城市 j ,满足 j != i 且 0 <= j < locations.length ,并移动到城市 j 。从城市 i 移动到 j 消耗的汽油量为 |locations[i] - locations[j]|,|x| 表示 x 的绝对值。
请注意, fuel 任何时刻都 不能 为负,且你 可以 经过任意城市超过一次(包括 start 和 finish )。
请你返回从 start 到 finish 所有可能路径的数目。
由于答案可能很大, 请将它对 10^9 + 7 取余后返回。
示例 1:
输入:locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5
输出:4
解释:以下为所有可能路径,每一条都用了 5 单位的汽油:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
示例 2:
输入:locations = [4,3,1], start = 1, finish = 0, fuel = 6
输出:5
解释:以下为所有可能的路径:
1 -> 0,使用汽油量为 fuel = 1
1 -> 2 -> 0,使用汽油量为 fuel = 5
1 -> 2 -> 1 -> 0,使用汽油量为 fuel = 5
1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 5
示例 3:
输入:locations = [5,2,1], start = 0, finish = 2, fuel = 3
输出:0
解释:没有办法只用 3 单位的汽油从 0 到达 2 。因为最短路径需要 4 单位的汽油。示例 4 :
输入:locations = [2,1,5], start = 0, finish = 0, fuel = 3
输出:2
解释:总共有两条可行路径,0 和 0 -> 1 -> 0 。示例 5:
输入:locations = [1,2,3], start = 0, finish = 2, fuel = 40
输出:615088286
解释:路径总数为 2615088300 。将结果对 10^9 + 7 取余,得到 615088286 。
提示:
2 <= locations.length <= 1001 <= locations[i] <= 10^9- 所有
locations中的整数 互不相同 。 0 <= start, finish < locations.length1 <= fuel <= 200
Metadata
- Link: Count All Possible Routes
- Difficulty: Hard
- Tag:
MemoizationArrayDynamic Programming
You are given an array of distinct positive integers locations where locations[i] represents the position of city i. You are also given integers start, finish and fuel representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city i, you can pick any city j such that j != i and 0 <= j < locations.length and move to city j. Moving from city i to city j reduces the amount of fuel you have by |locations[i] - locations[j]|. Please notice that |x| denotes the absolute value of x.
Notice that fuel cannot become negative at any point in time, and that you are allowed to visit any city more than once (including start and finish).
Return the count of all possible routes from start to finish. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
Input: locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5
Output: 4
Explanation: The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
Example 2:
Input: locations = [4,3,1], start = 1, finish = 0, fuel = 6
Output: 5
Explanation: The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5
Example 3:
Input: locations = [5,2,1], start = 0, finish = 2, fuel = 3
Output: 0
Explanation: It is impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.
Constraints:
2 <= locations.length <= 1001 <= locations[i] <= 109- All integers in
locationsare distinct. 0 <= start, finish < locations.length1 <= fuel <= 200
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 2e2 + 10;
int n;
int f[N][N];
int dis[N][N];
class Solution {
public:
int countRoutes(vector<int> &locations, int start, int finish, int _fuel) {
int fuel = _fuel;
n = SZ(locations);
memset(f, 0, sizeof f);
f[0][start] = 1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
if (j != i) {
dis[i][j] = abs(locations[i] - locations[j]);
}
}
for (int i = 0; i <= fuel; ++i) {
for (int j = 0; j < n; ++j)
if (f[i][j]) {
for (int k = 0; k < n; ++k)
if (j != k && i + dis[j][k] <= fuel) {
chadd(f[i + dis[j][k]][k], f[i][j]);
}
}
}
ll res = 0;
for (int i = 0; i <= fuel; ++i) {
chadd(res, f[i][finish]);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif