weekly-contest-289
A
Statement
Metadata
- Link: 计算字符串的数字和
- Difficulty: Easy
- Tag:
给你一个由若干数字(0 - 9)组成的字符串 s ,和一个整数。
如果 s 的长度大于 k ,则可以执行一轮操作。在一轮操作中,需要完成以下工作:
- 将
s拆分 成长度为k的若干 连续数字组 ,使得前k个字符都分在第一组,接下来的k个字符都分在第二组,依此类推。注意,最后一个数字组的长度可以小于k。 - 用表示每个数字组中所有数字之和的字符串来 替换 对应的数字组。例如,
"346"会替换为"13",因为3 + 4 + 6 = 13。 - 合并 所有组以形成一个新字符串。如果新字符串的长度大于
k则重复第一步。
返回在完成所有轮操作后的 s 。
示例 1:
输入:s = "11111222223", k = 3
输出:"135"
解释:
- 第一轮,将 s 分成:"111"、"112"、"222" 和 "23" 。
接着,计算每一组的数字和:1 + 1 + 1 = 3、1 + 1 + 2 = 4、2 + 2 + 2 = 6 和 2 + 3 = 5 。
这样,s 在第一轮之后变成 "3" + "4" + "6" + "5" = "3465" 。
- 第二轮,将 s 分成:"346" 和 "5" 。
接着,计算每一组的数字和:3 + 4 + 6 = 13 、5 = 5 。
这样,s 在第二轮之后变成 "13" + "5" = "135" 。
现在,s.length <= k ,所以返回 "135" 作为答案。
示例 2:
输入:s = "00000000", k = 3
输出:"000"
解释:
将 "000", "000", and "00".
接着,计算每一组的数字和:0 + 0 + 0 = 0 、0 + 0 + 0 = 0 和 0 + 0 = 0 。
s 变为 "0" + "0" + "0" = "000" ,其长度等于 k ,所以返回 "000" 。
提示:
1 <= s.length <= 1002 <= k <= 100s仅由数字(0-9)组成。
Metadata
- Link: Calculate Digit Sum of a String
- Difficulty: Easy
- Tag:
You are given a string s consisting of digits and an integer k.
A round can be completed if the length of s is greater than k. In one round, do the following:
- Divide
sinto consecutive groups of sizeksuch that the firstkcharacters are in the first group, the nextkcharacters are in the second group, and so on. Note that the size of the last group can be smaller thank. - Replace each group of
swith a string representing the sum of all its digits. For example,"346"is replaced with"13"because3 + 4 + 6 = 13. - Merge consecutive groups together to form a new string. If the length of the string is greater than
k, repeat from step1.
Return s after all rounds have been completed.
Example 1:
Input: s = "11111222223", k = 3
Output: "135"
Explanation:
- For the first round, we divide s into groups of size 3: "111", "112", "222", and "23".
Then we calculate the digit sum of each group: 1 + 1 + 1 = 3, 1 + 1 + 2 = 4, 2 + 2 + 2 = 6, and 2 + 3 = 5.
So, s becomes "3" + "4" + "6" + "5" = "3465" after the first round.
- For the second round, we divide s into "346" and "5".
Then we calculate the digit sum of each group: 3 + 4 + 6 = 13, 5 = 5.
So, s becomes "13" + "5" = "135" after second round.
Now, s.length <= k, so we return "135" as the answer.
Example 2:
Input: s = "00000000", k = 3
Output: "000"
Explanation:
We divide s into "000", "000", and "00".
Then we calculate the digit sum of each group: 0 + 0 + 0 = 0, 0 + 0 + 0 = 0, and 0 + 0 = 0.
s becomes "0" + "0" + "0" = "000", whose length is equal to k, so we return "000".
Constraints:
1 <= s.length <= 1002 <= k <= 100sconsists of digits only.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
string digitSum(string s, int k) {
const auto gao = [&](std::string s) {
int cur = 0;
string res = "";
for (int i = 0, j = 0; i <= s.length(); i++, j++) {
if (i == s.length() || j == k) {
res += to_string(cur);
cur = 0;
j = 0;
if (i == s.length()) {
break;
}
}
cur += s[i] - '0';
}
return res;
};
while (s.length() > k) {
s = gao(s);
}
return s;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 完成所有任务需要的最少轮数
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的整数数组 tasks ,其中 tasks[i] 表示任务的难度级别。在每一轮中,你可以完成 2 个或者 3 个 相同难度级别 的任务。
返回完成所有任务需要的 最少 轮数,如果无法完成所有任务,返回 -1 。
示例 1:
输入:tasks = [2,2,3,3,2,4,4,4,4,4]
输出:4
解释:要想完成所有任务,一个可能的计划是:
- 第一轮,完成难度级别为 2 的 3 个任务。
- 第二轮,完成难度级别为 3 的 2 个任务。
- 第三轮,完成难度级别为 4 的 3 个任务。
- 第四轮,完成难度级别为 4 的 2 个任务。
可以证明,无法在少于 4 轮的情况下完成所有任务,所以答案为 4 。
示例 2:
输入:tasks = [2,3,3]
输出:-1
解释:难度级别为 2 的任务只有 1 个,但每一轮执行中,只能选择完成 2 个或者 3 个相同难度级别的任务。因此,无法完成所有任务,答案为 -1 。
提示:
1 <= tasks.length <= 1051 <= tasks[i] <= 109
Metadata
- Link: Minimum Rounds to Complete All Tasks
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array tasks, where tasks[i] represents the difficulty level of a task. In each round, you can complete either 2 or 3 tasks of the same difficulty level.
Return the minimum rounds required to complete all the tasks, or -1 if it is not possible to complete all the tasks.
Example 1:
Input: tasks = [2,2,3,3,2,4,4,4,4,4]
Output: 4
Explanation: To complete all the tasks, a possible plan is:
- In the first round, you complete 3 tasks of difficulty level 2.
- In the second round, you complete 2 tasks of difficulty level 3.
- In the third round, you complete 3 tasks of difficulty level 4.
- In the fourth round, you complete 2 tasks of difficulty level 4.
It can be shown that all the tasks cannot be completed in fewer than 4 rounds, so the answer is 4.
Example 2:
Input: tasks = [2,3,3]
Output: -1
Explanation: There is only 1 task of difficulty level 2, but in each round, you can only complete either 2 or 3 tasks of the same difficulty level. Hence, you cannot complete all the tasks, and the answer is -1.
Constraints:
1 <= tasks.length <= 1051 <= tasks[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minimumRounds(vector<int> &tasks) {
map<int, int> mp;
for (auto &t : tasks) {
++mp[t];
}
int res = 0;
for (auto &[k, v] : mp) {
if (v == 1) {
return -1;
}
if (v <= 3) {
res += 1;
continue;
}
if (v % 3 == 0) {
res += v / 3;
} else if (v % 3 == 2) {
res += (v - 2) / 3 + 1;
} else if (v % 3 == 1) {
res += (v - 4) / 3 + 2;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 转角路径的乘积中最多能有几个尾随零
- Difficulty: Medium
- Tag:
给你一个二维整数数组 grid ,大小为 m x n,其中每个单元格都含一个正整数。
转角路径 定义为:包含至多一个弯的一组相邻单元。具体而言,路径应该完全 向水平方向 或者 向竖直方向 移动过弯(如果存在弯),而不能访问之前访问过的单元格。在过弯之后,路径应当完全朝 另一个 方向行进:如果之前是向水平方向,那么就应该变为向竖直方向;反之亦然。当然,同样不能访问之前已经访问过的单元格。
一条路径的 乘积 定义为:路径上所有值的乘积。
请你从 grid 中找出一条乘积中尾随零数目最多的转角路径,并返回该路径中尾随零的数目。
注意:
- 水平 移动是指向左或右移动。
- 竖直 移动是指向上或下移动。
示例 1:
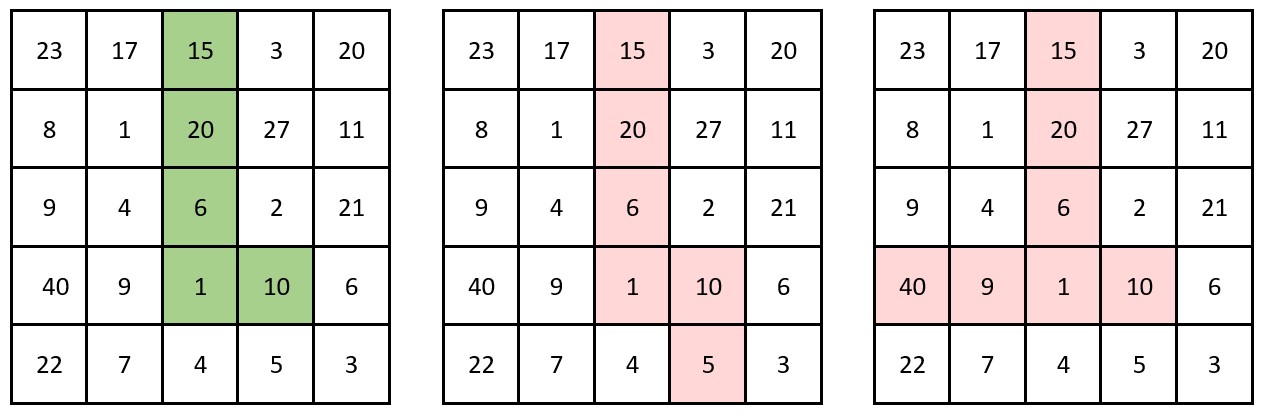
输入:grid = [[23,17,15,3,20],[8,1,20,27,11],[9,4,6,2,21],[40,9,1,10,6],[22,7,4,5,3]]
输出:3
解释:左侧的图展示了一条有效的转角路径。
其乘积为 15 * 20 * 6 * 1 * 10 = 18000 ,共计 3 个尾随零。
可以证明在这条转角路径的乘积中尾随零数目最多。
中间的图不是一条有效的转角路径,因为它有不止一个弯。
右侧的图也不是一条有效的转角路径,因为它需要重复访问已经访问过的单元格。
示例 2:
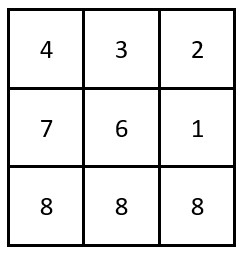
输入:grid = [[4,3,2],[7,6,1],[8,8,8]]
输出:0
解释:网格如上图所示。
不存在乘积含尾随零的转角路径。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1051 <= grid[i][j] <= 1000
Metadata
- Link: Maximum Trailing Zeros in a Cornered Path
- Difficulty: Medium
- Tag:
You are given a 2D integer array grid of size m x n, where each cell contains a positive integer.
A cornered path is defined as a set of adjacent cells with at most one turn. More specifically, the path should exclusively move either horizontally or vertically up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the alternate direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The product of a path is defined as the product of all the values in the path.
Return the maximum number of trailing zeros in the product of a cornered path found in grid.
Note:
- Horizontal movement means moving in either the left or right direction.
- Vertical movement means moving in either the up or down direction.
Example 1:

Input: grid = [[23,17,15,3,20],[8,1,20,27,11],[9,4,6,2,21],[40,9,1,10,6],[22,7,4,5,3]]
Output: 3
Explanation: The grid on the left shows a valid cornered path.
It has a product of 15 * 20 * 6 * 1 * 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
Example 2:

Input: grid = [[4,3,2],[7,6,1],[8,8,8]]
Output: 0
Explanation: The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1051 <= grid[i][j] <= 1000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 1e3 + 10;
PII h[N];
class Solution {
public:
void init() {
for (int i = 2; i <= 1000; i++) {
int x = i;
while (x) {
if (x % 2 == 0) {
x /= 2;
++h[i].first;
} else if (x % 5 == 0) {
x /= 5;
++h[i].second;
} else {
break;
}
}
}
}
int maxTrailingZeros(vector<vector<int>> &grid) {
if (h[2] != PII(1, 0)) {
init();
}
int n = grid.size();
int m = grid[0].size();
auto f = vector<vector<PII>>(n + 1, vector<PII>(m + 1, PII(0, 0)));
auto g = vector<vector<PII>>(n + 1, vector<PII>(m + 1, PII(0, 0)));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int x = grid[i][j];
if (!j) {
f[i][j] = h[x];
} else {
f[i][j] = PII(f[i][j - 1].first + h[x].first, f[i][j - 1].second + h[x].second);
}
}
for (int j = m - 1; j >= 0; j--) {
int x = grid[i][j];
if (j == m - 1) {
g[i][j] = h[x];
} else {
g[i][j] = PII(g[i][j + 1].first + h[x].first, g[i][j + 1].second + h[x].second);
}
}
}
int res = 0;
for (int j = 0; j < m; j++) {
{
PII now(0, 0);
for (int i = 0; i < n; i++) {
{
PII cur = now;
cur.first += f[i][j].first;
cur.second += f[i][j].second;
int y = min(cur.first, cur.second);
if (y > res) {
res = y;
}
}
{
PII cur = now;
cur.first += g[i][j].first;
cur.second += g[i][j].second;
int y = min(cur.first, cur.second);
if (y > res) {
res = y;
}
}
int x = grid[i][j];
now.first += h[x].first;
now.second += h[x].second;
}
}
{
PII now(0, 0);
for (int i = n - 1; i >= 0; i--) {
{
PII cur = now;
cur.first += f[i][j].first;
cur.second += f[i][j].second;
int y = min(cur.first, cur.second);
if (y > res) {
res = y;
}
}
{
PII cur = now;
cur.first += g[i][j].first;
cur.second += g[i][j].second;
int y = min(cur.first, cur.second);
if (y > res) {
res = y;
}
}
int x = grid[i][j];
now.first += h[x].first;
now.second += h[x].second;
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 相邻字符不同的最长路径
- Difficulty: Hard
- Tag:
给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
示例 1:
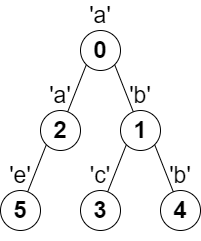
输入:parent = [-1,0,0,1,1,2], s = "abacbe"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。
示例 2:
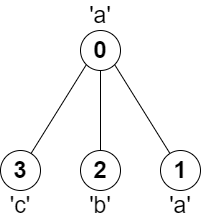
输入:parent = [-1,0,0,0], s = "aabc"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
n == parent.length == s.length1 <= n <= 105- 对所有
i >= 1,0 <= parent[i] <= n - 1均成立 parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
Metadata
- Link: Longest Path With Different Adjacent Characters
- Difficulty: Hard
- Tag:
You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to n - 1. The tree is represented by a 0-indexed array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.
You are also given a string s of length n, where s[i] is the character assigned to node i.
Return the length of the longest path in the tree such that no pair of adjacent nodes on the path have the same character assigned to them.
Example 1:

Input: parent = [-1,0,0,1,1,2], s = "abacbe"
Output: 3
Explanation: The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
Example 2:

Input: parent = [-1,0,0,0], s = "aabc"
Output: 3
Explanation: The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
Constraints:
n == parent.length == s.length1 <= n <= 1050 <= parent[i] <= n - 1for alli >= 1parent[0] == -1parentrepresents a valid tree.sconsists of only lowercase English letters.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> f;
string s;
vector<vector<int>> G;
int res;
int dfs(int rt) {
int cur = 1;
vector<int> ff;
for (const auto &v : G[rt]) {
int curr = dfs(v);
if (s[rt] == s[v]) {
continue;
}
ff.push_back(curr);
}
sort(all(ff));
reverse(all(ff));
if (ff.size() >= 1) {
cur += ff[0];
res = max(res, cur);
}
if (ff.size() >= 2) {
res = max(res, ff[0] + ff[1] + 1);
}
return cur;
}
int longestPath(vector<int> &f, string s) {
this->f = f;
this->s = s;
res = 1;
int n = f.size();
G = vector<vector<int>>(n + 1, vector<int>());
for (int i = 1; i < n; i++) {
G[f[i]].push_back(i);
}
dfs(0);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif