biweekly-contest-71

A

Statement

简体中文English

Metadata

Link: 拆分数位后四位数字的最小和
Difficulty: Easy
Tag: 贪心 数学 排序

给你一个四位正整数 num 。请你使用 num 中的数位，将 num 拆成两个新的整数 new1 和 new2 。new1 和 new2 中可以有 前导 0 ，且 num 中所有数位都必须使用。

比方说，给你 num = 2932 ，你拥有的数位包括：两个 2 ，一个 9 和一个 3 。一些可能的 [new1, new2] 数对为 [22, 93]，[23, 92]，[223, 9] 和 [2, 329] 。

请你返回可以得到的 new1 和 new2 的最小和。

示例 1：

输入：num = 2932
输出：52
解释：可行的 [new1, new2] 数对为 [29, 23] ，[223, 9] 等等。
最小和为数对 [29, 23] 的和：29 + 23 = 52 。

示例 2：

输入：num = 4009
输出：13
解释：可行的 [new1, new2] 数对为 [0, 49] ，[490, 0] 等等。
最小和为数对 [4, 9] 的和：4 + 9 = 13 。

提示：

1000 <= num <= 9999

Metadata

Link: Minimum Sum of Four Digit Number After Splitting Digits
Difficulty: Easy
Tag: Greedy Math Sorting

You are given a positive integer num consisting of exactly four digits. Split num into two new integers new1 and new2 by using the digits found in num. Leading zeros are allowed in new1 and new2, and all the digits found in num must be used.

For example, given num = 2932, you have the following digits: two 2's, one 9 and one 3. Some of the possible pairs [new1, new2] are [22, 93], [23, 92], [223, 9] and [2, 329].

Return the minimum possible sum of new1 and new2.

Example 1:

Input: num = 2932
Output: 52
Explanation: Some possible pairs [new1, new2] are [29, 23], [223, 9], etc.
The minimum sum can be obtained by the pair [29, 23]: 29 + 23 = 52.

Example 2:

Input: num = 4009
Output: 13
Explanation: Some possible pairs [new1, new2] are [0, 49], [490, 0], etc. 
The minimum sum can be obtained by the pair [4, 9]: 4 + 9 = 13.

Constraints:

1000 <= num <= 9999

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int minimumSum(int num) {
        string s = to_string(num);
        sort(all(s));
        int res = num;

        auto f = [](const string &s) {
            int res = 0;
            for (auto &c : s) {
                res = res * 10 + (c - '0');
            }

            return res;
        };

        do {
            for (int i = 0; i < 4; i++) {
                int now = f(s.substr(0, i)) + f(s.substr(i, 4 - i));
                chmin(res, now);
            }
        } while (next_permutation(all(s)));

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 根据给定数字划分数组
Difficulty: Medium
Tag: 数组 双指针 模拟

给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列，使得以下条件均成立：

所有小于 pivot 的元素都出现在所有大于 pivot 的元素之前。
所有等于 pivot 的元素都出现在小于和大于 pivot 的元素中间。
小于 pivot 的元素之间和大于 pivot 的元素之间的 相对顺序 不发生改变。
- 更正式的，考虑每一对 p_i，p_j ，p_i 是初始时位置 i 元素的新位置，p_j 是初始时位置 j 元素的新位置。对于小于 pivot 的元素，如果 i < j 且 nums[i] < pivot 和 nums[j] < pivot 都成立，那么 p_i < p_j 也成立。类似的，对于大于 pivot 的元素，如果 i < j 且 nums[i] > pivot 和 nums[j] > pivot 都成立，那么 p_i < p_j 。

请你返回重新排列 nums 数组后的结果数组。

示例 1：

输入：nums = [9,12,5,10,14,3,10], pivot = 10
输出：[9,5,3,10,10,12,14]
解释：
元素 9 ，5 和 3 小于 pivot ，所以它们在数组的最左边。
元素 12 和 14 大于 pivot ，所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ，它们在结果数组中的相对顺序需要保留。

示例 2：

输入：nums = [-3,4,3,2], pivot = 2
输出：[-3,2,4,3]
解释：
元素 -3 小于 pivot ，所以在数组的最左边。
元素 4 和 3 大于 pivot ，所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [-3] 和 [4, 3] ，它们在结果数组中的相对顺序需要保留。

提示：

1 <= nums.length <= 10⁵
-10⁶ <= nums[i] <= 10⁶
pivot 等于 nums 中的一个元素。

Metadata

Link: Partition Array According to Given Pivot
Difficulty: Medium
Tag: Array Two Pointers Simulation

You are given a 0-indexed integer array nums and an integer pivot. Rearrange nums such that the following conditions are satisfied:

Every element less than pivot appears before every element greater than pivot.
Every element equal to pivot appears in between the elements less than and greater than pivot.
The relative order of the elements less than pivot and the elements greater than pivot is maintained.
- More formally, consider every p_i, p_j where p_i is the new position of the i^th element and p_j is the new position of the j^th element. For elements less than pivot, if i < j and nums[i] < pivot and nums[j] < pivot, then p_i < p_j. Similarly for elements greater than pivot, if i < j and nums[i] > pivot and nums[j] > pivot, then p_i < p_j.

Return nums after the rearrangement.

Example 1:

Input: nums = [9,12,5,10,14,3,10], pivot = 10
Output: [9,5,3,10,10,12,14]
Explanation: 
The elements 9, 5, and 3 are less than the pivot so they are on the left side of the array.
The elements 12 and 14 are greater than the pivot so they are on the right side of the array.
The relative ordering of the elements less than and greater than pivot is also maintained. [9, 5, 3] and [12, 14] are the respective orderings.

Example 2:

Input: nums = [-3,4,3,2], pivot = 2
Output: [-3,2,4,3]
Explanation: 
The element -3 is less than the pivot so it is on the left side of the array.
The elements 4 and 3 are greater than the pivot so they are on the right side of the array.
The relative ordering of the elements less than and greater than pivot is also maintained. [-3] and [4, 3] are the respective orderings.

Constraints:

1 <= nums.length <= 10⁵
-10⁶ <= nums[i] <= 10⁶
pivot equals to an element of nums.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

struct node {
    int ix;
    int num;
};

class Solution {
public:
    vector<int> pivotArray(vector<int> &nums, int pivot) {
        vector<node> vec;
        for (int i = 0; i < nums.size(); i++) {
            vec.emplace_back(node{.ix = i, .num = nums[i]});
        }

        const auto sgn = [&](int x) {
            if (x < pivot) {
                return -1;
            }

            if (x == pivot) {
                return 0;
            }

            return 1;
        };

        sort(all(vec), [&](const node &a, const node &b) {
            if (sgn(a.num) != sgn(b.num)) {
                return sgn(a.num) < sgn(b.num);
            }

            return a.ix < b.ix;
        });

        vector<int> res;

        for (const auto &a : vec) {
            res.push_back(a.num);
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 设置时间的最少代价
Difficulty: Medium
Tag: 数学 枚举

常见的微波炉可以设置加热时间，且加热时间满足以下条件：

至少为 1 秒钟。
至多为 99 分 99 秒。

你可以最多输入 4 个数字 来设置加热时间。如果你输入的位数不足 4 位，微波炉会自动加前缀 0 来补足 4 位。微波炉会将设置好的四位数中，前两位当作分钟数，后两位当作秒数。它们所表示的总时间就是加热时间。比方说：

你输入 9 5 4 （三个数字），被自动补足为 0954 ，并表示 9 分 54 秒。
你输入 0 0 0 8 （四个数字），表示 0 分 8 秒。
你输入 8 0 9 0 ，表示 80 分 90 秒。
你输入 8 1 3 0 ，表示 81 分 30 秒。

给你整数 startAt ，moveCost ，pushCost 和 targetSeconds 。一开始，你的手指在数字 startAt 处。将手指移到 任何其他数字 ，需要花费 moveCost 的单位代价。每输入你手指所在位置的数字一次，需要花费 pushCost 的单位代价。

要设置 targetSeconds 秒的加热时间，可能会有多种设置方法。你想要知道这些方法中，总代价最小为多少。

请你能返回设置 targetSeconds 秒钟加热时间需要花费的最少代价。

请记住，虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒。

示例 1：

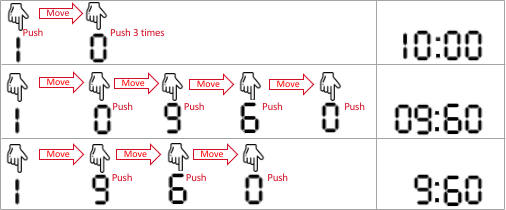
输入：startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
输出：6
解释：以下为设置加热时间的所有方法。
- 1 0 0 0 ，表示 10 分 0 秒。
  手指一开始就在数字 1 处，输入 1 （代价为 1），移到 0 处（代价为 2），输入 0（代价为 1），输入 0（代价为 1），输入 0（代价为 1）。
  总代价为：1 + 2 + 1 + 1 + 1 = 6 。这是所有方案中的最小代价。
- 0 9 6 0，表示 9 分 60 秒。它也表示 600 秒。
  手指移到 0 处（代价为 2），输入 0 （代价为 1），移到 9 处（代价为 2），输入 9（代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12 。
- 9 6 0，微波炉自动补全为 0960 ，表示 9 分 60 秒。
  手指移到 9 处（代价为 2），输入 9 （代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 = 9 。

示例 2：

输入：startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
输出：6
解释：最优方案为输入两个数字 7 6，表示 76 秒。
手指移到 7 处（代价为 1），输入 7 （代价为 2），移到 6 处（代价为 1），输入 6（代价为 2）。总代价为：1 + 2 + 1 + 2 = 6
其他可行方案为 0076 ，076 ，0116 和 116 ，但是它们的代价都比 6 大。

提示：

0 <= startAt <= 9
1 <= moveCost, pushCost <= 10⁵
1 <= targetSeconds <= 6039

Metadata

Link: Minimum Cost to Set Cooking Time
Difficulty: Medium
Tag: Math Enumeration

A generic microwave supports cooking times for:

at least 1 second.
at most 99 minutes and 99 seconds.

To set the cooking time, you push at most four digits. The microwave normalizes what you push as four digits by prepending zeroes. It interprets the first two digits as the minutes and the last two digits as the seconds. It then adds them up as the cooking time. For example,

You push 9 5 4 (three digits). It is normalized as 0954 and interpreted as 9 minutes and 54 seconds.
You push 0 0 0 8 (four digits). It is interpreted as 0 minutes and 8 seconds.
You push 8 0 9 0. It is interpreted as 80 minutes and 90 seconds.
You push 8 1 3 0. It is interpreted as 81 minutes and 30 seconds.

You are given integers startAt, moveCost, pushCost, and targetSeconds. Initially, your finger is on the digit startAt. Moving the finger above any specific digit costs moveCost units of fatigue. Pushing the digit below the finger once costs pushCost units of fatigue.

There can be multiple ways to set the microwave to cook for targetSeconds seconds but you are interested in the way with the minimum cost.

Return the minimum cost to set targetSeconds seconds of cooking time.

Remember that one minute consists of 60 seconds.

Example 1:

Input: startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
Output: 6
Explanation: The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
  The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
  The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
  The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
  The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
  The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
  The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.

Example 2:

Input: startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
Output: 6
Explanation: The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.

Constraints:

0 <= startAt <= 9
1 <= moveCost, pushCost <= 10⁵
1 <= targetSeconds <= 6039

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
        const auto calc = [&](const string &s) -> int {
            int cur = startAt;
            int cost = 0;
            for (const auto &c : s) {
                if (cost == 0 && c == '0') {
                    continue;
                }

                int now = c - '0';
                if (now != cur) {
                    cur = now;
                    cost += moveCost;
                }

                cost += pushCost;
            }

            dbg(s, cost);

            return cost;
        };

        int a = targetSeconds / 60;
        int b = targetSeconds % 60;

        int cost = 99999999;

        if (a <= 99) {
            chmin(cost, calc(to_string(a) + ((b <= 9 ? string("0") : string("")) + to_string(b))));
        }

        if (a >= 1 && b <= 39) {
            chmin(cost, calc(to_string(a - 1) + to_string(b + 60)));
        }

        return cost;
    }
};

#ifdef LOCAL

int main() {
    auto s = new Solution();
    {
        auto ans = s->minCostSetTime(5, 15, 20, 365);
        assert_eq(ans, 90);
    }
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 删除元素后和的最小差值
Difficulty: Hard
Tag: 数组 动态规划 堆（优先队列）

给你一个下标从 0 开始的整数数组 nums ，它包含 3 * n 个元素。

你可以从 nums 中删除恰好 n 个元素，剩下的 2 * n 个元素将会被分成两个 相同大小 的部分。

前面 n 个元素属于第一部分，它们的和记为 sum_first 。
后面 n 个元素属于第二部分，它们的和记为 sum_second 。

两部分和的差值记为 sum_first - sum_second 。

比方说，sum_first = 3 且 sum_second = 2 ，它们的差值为 1 。
再比方，sum_first = 2 且 sum_second = 3 ，它们的差值为 -1 。

请你返回删除 n 个元素之后，剩下两部分和的 差值的最小值 是多少。

示例 1：

输入：nums = [3,1,2]
输出：-1
解释：nums 有 3 个元素，所以 n = 1 。
所以我们需要从 nums 中删除 1 个元素，并将剩下的元素分成两部分。
- 如果我们删除 nums[0] = 3 ，数组变为 [1,2] 。两部分和的差值为 1 - 2 = -1 。
- 如果我们删除 nums[1] = 1 ，数组变为 [3,2] 。两部分和的差值为 3 - 2 = 1 。
- 如果我们删除 nums[2] = 2 ，数组变为 [3,1] 。两部分和的差值为 3 - 1 = 2 。
两部分和的最小差值为 min(-1,1,2) = -1 。

示例 2：

输入：nums = [7,9,5,8,1,3]
输出：1
解释：n = 2 。所以我们需要删除 2 个元素，并将剩下元素分为 2 部分。
如果我们删除元素 nums[2] = 5 和 nums[3] = 8 ，剩下元素为 [7,9,1,3] 。和的差值为 (7+9) - (1+3) = 12 。
为了得到最小差值，我们应该删除 nums[1] = 9 和 nums[4] = 1 ，剩下的元素为 [7,5,8,3] 。和的差值为 (7+5) - (8+3) = 1 。
观察可知，最优答案为 1 。

提示：

nums.length == 3 * n
1 <= n <= 10⁵
1 <= nums[i] <= 10⁵

Metadata

Link: Minimum Difference in Sums After Removal of Elements
Difficulty: Hard
Tag: Array Dynamic Programming Heap (Priority Queue)

You are given a 0-indexed integer array nums consisting of 3 * n elements.

You are allowed to remove any subsequence of elements of size exactly n from nums. The remaining 2 * n elements will be divided into two equal parts:

The first n elements belonging to the first part and their sum is sum_first.
The next n elements belonging to the second part and their sum is sum_second.

The difference in sums of the two parts is denoted as sum_first - sum_second.

For example, if sum_first = 3 and sum_second = 2, their difference is 1.
Similarly, if sum_first = 2 and sum_second = 3, their difference is -1.

Return the minimum difference possible between the sums of the two parts after the removal of n elements.

Example 1:

Input: nums = [3,1,2]
Output: -1
Explanation: Here, nums has 3 elements, so n = 1. 
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums[0] = 3, the array will be [1,2]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums[1] = 1, the array will be [3,2]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums[2] = 2, the array will be [3,1]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.

Example 2:

Input: nums = [7,9,5,8,1,3]
Output: 1
Explanation: Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums[2] = 5 and nums[3] = 8, the resultant array will be [7,9,1,3]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums[1] = 9 and nums[4] = 1. The resultant array becomes [7,5,8,3]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.

Constraints:

nums.length == 3 * n
1 <= n <= 10⁵
1 <= nums[i] <= 10⁵

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

const ll INF = 0x3f3f3f3f3f3f3f3f;

class Solution {
public:
    long long minimumDifference(vector<int> &nums) {
        ll res = INF;
        int n = nums.size() / 3;

        vector<ll> lsum(n * 3, 0), rsum(n * 3, 0);

        {
            ll sum = 0;
            multiset<int> s;
            for (int i = 0; i <= n - 1; i++) {
                sum += nums[i];
                s.insert(nums[i]);
            }

            lsum[n - 1] = sum;
            for (int i = n; i < n * 2; i++) {
                int a = nums[i];
                s.insert(a);
                sum += a;
                sum -= *(s.rbegin());
                lsum[i] = sum;
                s.erase(s.find(*(s.rbegin())));
            }
        }

        {
            ll sum = 0;
            multiset<int> s;
            for (int i = n * 3 - 1; i >= n * 2; i--) {
                sum += nums[i];
                s.insert(nums[i]);
            }

            rsum[n * 2] = sum;
            for (int i = n * 2 - 1; i >= n; i--) {
                int a = nums[i];
                s.insert(a);
                sum += a;
                sum -= *(s.begin());
                rsum[i] = sum;
                s.erase(s.find(*(s.begin())));
            }
        }

        dbg(lsum, rsum);

        for (int i = n - 1; i < n * 2; i++) {
            chmin(res, lsum[i] - rsum[i + 1]);
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    auto s = new Solution();

    {
        auto vec = vector<int>({3, 1, 2});
        auto ans = s->minimumDifference(vec);
        assert_eq(ans, ll(-1));
    }

    {
        auto vec = vector<int>({7, 9, 5, 8, 1, 3});
        auto ans = s->minimumDifference(vec);
        assert_eq(ans, ll(1));
    }
    return 0;
}

#endif

最后更新: October 11, 2023