weekly-contest-213
A
Statement
Metadata
- Link: 能否连接形成数组
- Difficulty: Easy
- Tag:
数组哈希表
给你一个整数数组 arr ,数组中的每个整数 互不相同 。另有一个由整数数组构成的数组 pieces,其中的整数也 互不相同 。请你以 任意顺序 连接 pieces 中的数组以形成 arr 。但是,不允许 对每个数组 pieces[i] 中的整数重新排序。
如果可以连接 pieces 中的数组形成 arr ,返回 true ;否则,返回 false 。
示例 1:
输入:arr = [85], pieces = [[85]]
输出:true
示例 2:
输入:arr = [15,88], pieces = [[88],[15]]
输出:true
解释:依次连接 [15] 和 [88]
示例 3:
输入:arr = [49,18,16], pieces = [[16,18,49]]
输出:false
解释:即便数字相符,也不能重新排列 pieces[0]
示例 4:
输入:arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
输出:true
解释:依次连接 [91]、[4,64] 和 [78]示例 5:
输入:arr = [1,3,5,7], pieces = [[2,4,6,8]]
输出:false
提示:
1 <= pieces.length <= arr.length <= 100sum(pieces[i].length) == arr.length1 <= pieces[i].length <= arr.length1 <= arr[i], pieces[i][j] <= 100arr中的整数 互不相同pieces中的整数 互不相同(也就是说,如果将pieces扁平化成一维数组,数组中的所有整数互不相同)
Metadata
- Link: Check Array Formation Through Concatenation
- Difficulty: Easy
- Tag:
ArrayHash Table
You are given an array of distinct integers arr and an array of integer arrays pieces, where the integers in pieces are distinct. Your goal is to form arr by concatenating the arrays in pieces in any order. However, you are not allowed to reorder the integers in each array pieces[i].
Return true if it is possible to form the array arr from pieces. Otherwise, return false.
Example 1:
Input: arr = [15,88], pieces = [[88],[15]]
Output: true
Explanation: Concatenate [15] then [88]
Example 2:
Input: arr = [49,18,16], pieces = [[16,18,49]]
Output: false
Explanation: Even though the numbers match, we cannot reorder pieces[0].
Example 3:
Input: arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
Output: true
Explanation: Concatenate [91] then [4,64] then [78]
Constraints:
1 <= pieces.length <= arr.length <= 100sum(pieces[i].length) == arr.length1 <= pieces[i].length <= arr.length1 <= arr[i], pieces[i][j] <= 100- The integers in
arrare distinct. - The integers in
piecesare distinct (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct).
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1& x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1& x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1& x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T& arg, Ts&... args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t>& arg, const A&... args) {
for (auto& v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T& arg, const Ts&... args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T& arg, const Ts&... args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t>& arg, const A&... args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {
map<int, int> mp;
for (int i = 0; i < SZ(arr); ++i) {
mp[arr[i]] = i;
}
for (auto vec : pieces) {
for (int i = 1; i < SZ(vec); ++i) {
if (mp[vec[i]] != mp[vec[i - 1]] + 1)
return false;
}
}
return true;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 统计字典序元音字符串的数目
- Difficulty: Medium
- Tag:
动态规划
给你一个整数 n,请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。
字符串 s 按 字典序排列 需要满足:对于所有有效的 i,s[i] 在字母表中的位置总是与 s[i+1] 相同或在 s[i+1] 之前。
示例 1:
输入:n = 1
输出:5
解释:仅由元音组成的 5 个字典序字符串为 ["a","e","i","o","u"]
示例 2:
输入:n = 2
输出:15
解释:仅由元音组成的 15 个字典序字符串为
["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"]
注意,"ea" 不是符合题意的字符串,因为 'e' 在字母表中的位置比 'a' 靠后
示例 3:
输入:n = 33
输出:66045
提示:
1 <= n <= 50
Metadata
- Link: Count Sorted Vowel Strings
- Difficulty: Medium
- Tag:
Dynamic Programming
Given an integer n, return the number of strings of length n that consist only of vowels (a, e, i, o, u) and are lexicographically sorted.
A string s is lexicographically sorted if for all valid i, s[i] is the same as or comes before s[i+1] in the alphabet.
Example 1:
Input: n = 1
Output: 5
Explanation: The 5 sorted strings that consist of vowels only are ["a","e","i","o","u"].
Example 2:
Input: n = 2
Output: 15
Explanation: The 15 sorted strings that consist of vowels only are
["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"].
Note that "ea" is not a valid string since 'e' comes after 'a' in the alphabet.
Example 3:
Input: n = 33
Output: 66045
Constraints:
1 <= n <= 50
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
int f[N][10];
class Solution {
public:
int countVowelStrings(int n) {
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= n + 1; ++i) {
for (int j = 1; j <= 5; ++j) {
for (int k = 0; k <= j; ++k) {
f[i][j] += f[i - 1][k];
}
}
}
return f[n + 1][5];
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 可以到达的最远建筑
- Difficulty: Medium
- Tag:
贪心数组堆(优先队列)
给你一个整数数组 heights ,表示建筑物的高度。另有一些砖块 bricks 和梯子 ladders 。
你从建筑物 0 开始旅程,不断向后面的建筑物移动,期间可能会用到砖块或梯子。
当从建筑物 i 移动到建筑物 i+1(下标 从 0 开始 )时:
- 如果当前建筑物的高度 大于或等于 下一建筑物的高度,则不需要梯子或砖块
- 如果当前建筑的高度 小于 下一个建筑的高度,您可以使用 一架梯子 或
(h[i+1] - h[i])个砖块
示例 1:

输入:heights = [4,2,7,6,9,14,12], bricks = 5, ladders = 1
输出:4
解释:从建筑物 0 出发,你可以按此方案完成旅程:
- 不使用砖块或梯子到达建筑物 1 ,因为 4 >= 2
- 使用 5 个砖块到达建筑物 2 。你必须使用砖块或梯子,因为 2 < 7
- 不使用砖块或梯子到达建筑物 3 ,因为 7 >= 6
- 使用唯一的梯子到达建筑物 4 。你必须使用砖块或梯子,因为 6 < 9
无法越过建筑物 4 ,因为没有更多砖块或梯子。
示例 2:
输入:heights = [4,12,2,7,3,18,20,3,19], bricks = 10, ladders = 2
输出:7
示例 3:
输入:heights = [14,3,19,3], bricks = 17, ladders = 0
输出:3
提示:
1 <= heights.length <= 1051 <= heights[i] <= 1060 <= bricks <= 1090 <= ladders <= heights.length
Metadata
- Link: Furthest Building You Can Reach
- Difficulty: Medium
- Tag:
GreedyArrayHeap (Priority Queue)
You are given an integer array heights representing the heights of buildings, some bricks, and some ladders.
You start your journey from building 0 and move to the next building by possibly using bricks or ladders.
While moving from building i to building i+1 (0-indexed),
- If the current building's height is greater than or equal to the next building's height, you do not need a ladder or bricks.
- If the current building's height is less than the next building's height, you can either use one ladder or
(h[i+1] - h[i])bricks.
Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally.
Example 1:

Input: heights = [4,2,7,6,9,14,12], bricks = 5, ladders = 1
Output: 4
Explanation: Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
Example 2:
Input: heights = [4,12,2,7,3,18,20,3,19], bricks = 10, ladders = 2
Output: 7
Example 3:
Input: heights = [14,3,19,3], bricks = 17, ladders = 0
Output: 3
Constraints:
1 <= heights.length <= 1051 <= heights[i] <= 1060 <= bricks <= 1090 <= ladders <= heights.length
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
vector<int> heights;
int bricks, ladders;
bool ok(int x) {
vector<int> vec;
for (int i = 1; i <= x; ++i) {
if (heights[i] > heights[i - 1]) {
vec.push_back(heights[i] - heights[i - 1]);
}
}
sort(all(vec));
reverse(all(vec));
int has = bricks;
while (!vec.empty() && has >= vec.back()) {
has -= vec.back();
vec.pop_back();
}
return SZ(vec) <= ladders;
}
class Solution {
public:
int furthestBuilding(vector<int> &_heights, int _bricks, int _ladders) {
heights = _heights;
bricks = _bricks;
ladders = _ladders;
n = SZ(heights);
int l = 0, r = n - 1, res = l;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (ok(mid)) {
l = mid + 1;
res = mid;
} else {
r = mid - 1;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 第 K 条最小指令
- Difficulty: Hard
- Tag:
数组数学动态规划组合数学
Bob 站在单元格 (0, 0) ,想要前往目的地 destination :(row, column) 。他只能向 右 或向 下 走。你可以为 Bob 提供导航 指令 来帮助他到达目的地 destination 。
指令 用字符串表示,其中每个字符:
'H',意味着水平向右移动'V',意味着竖直向下移动
能够为 Bob 导航到目的地 destination 的指令可以有多种,例如,如果目的地 destination 是 (2, 3),"HHHVV" 和 "HVHVH" 都是有效 指令 。
然而,Bob 很挑剔。因为他的幸运数字是 k,他想要遵循 按字典序排列后的第 k 条最小指令 的导航前往目的地 destination 。k 的编号 从 1 开始 。
给你一个整数数组 destination 和一个整数 k ,请你返回可以为 Bob 提供前往目的地 destination 导航的 按字典序排列后的第 k 条最小指令 。
示例 1:
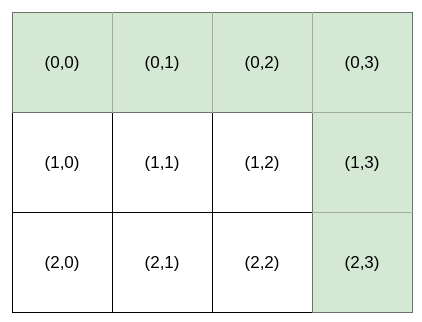
输入:destination = [2,3], k = 1
输出:"HHHVV"
解释:能前往 (2, 3) 的所有导航指令 按字典序排列后 如下所示:
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH", "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"].
示例 2:
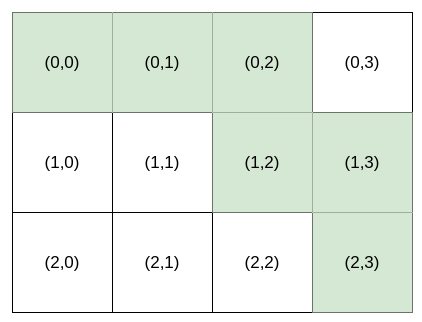
输入:destination = [2,3], k = 2
输出:"HHVHV"
示例 3:
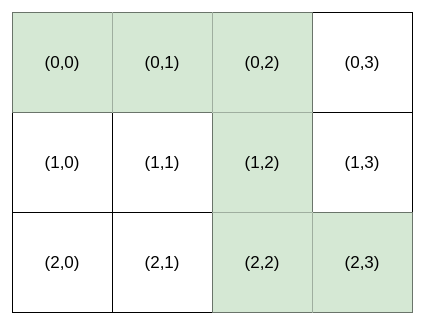
输入:destination = [2,3], k = 3
输出:"HHVVH"
提示:
destination.length == 21 <= row, column <= 151 <= k <= nCr(row + column, row),其中nCr(a, b)表示组合数,即从a个物品中选b个物品的不同方案数。
Metadata
- Link: Kth Smallest Instructions
- Difficulty: Hard
- Tag:
ArrayMathDynamic ProgrammingCombinatorics
Bob is standing at cell (0, 0), and he wants to reach destination: (row, column). He can only travel right and down. You are going to help Bob by providing instructions for him to reach destination.
The instructions are represented as a string, where each character is either:
'H', meaning move horizontally (go right), or'V', meaning move vertically (go down).
Multiple instructions will lead Bob to destination. For example, if destination is (2, 3), both "HHHVV" and "HVHVH" are valid instructions.
However, Bob is very picky. Bob has a lucky number k, and he wants the kth lexicographically smallest instructions that will lead him to destination. k is 1-indexed.
Given an integer array destination and an integer k, return the kth lexicographically smallest instructions that will take Bob to destination.
Example 1:
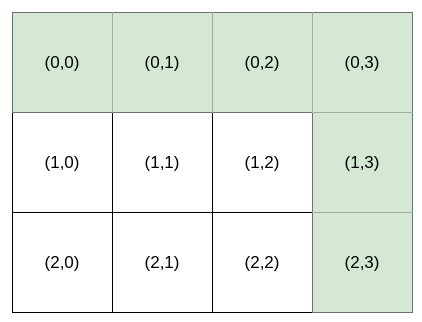
Input: destination = [2,3], k = 1
Output: "HHHVV"
Explanation: All the instructions that reach (2, 3) in lexicographic order are as follows:
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH", "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"].
Example 2:
Input: destination = [2,3], k = 2
Output: "HHVHV"
Example 3:
Input: destination = [2,3], k = 3
Output: "HHVVH"
Constraints:
destination.length == 21 <= row, column <= 151 <= k <= nCr(row + column, row), wherenCr(a, b)denotesachooseb.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
int x, y;
ll f[50][50];
void init() {
memset(f, 0, sizeof f);
for (int i = 0; i < 50; ++i) f[i][0] = f[i][i] = 1;
for (int i = 1; i < 50; ++i) {
for (int j = 1; j < 50; ++j) {
f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}
}
}
class Solution {
public:
string kthSmallestPath(vector<int> &destination, ll k) {
init();
x = destination[0];
y = destination[1];
swap(x, y);
n = x + y;
string res = "";
int _x = x, _y = y;
for (int i = 1; i <= n; ++i) {
if (!_x) {
res += 'V';
_y -= 1;
} else {
if (_y) {
ll now = f[n - i][_x - 1];
if (now < k) {
k -= now;
res += 'V';
_y -= 1;
} else {
res += 'H';
_x -= 1;
}
} else {
res += 'H';
_x -= 1;
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif