weekly-contest-203

A

Statement

简体中文English

Metadata

Link: 圆形赛道上经过次数最多的扇区
Difficulty: Easy
Tag: 数组 模拟

给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成，扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛，该马拉松全程由 m 个阶段组成。其中，第 i 个阶段将会从扇区 rounds[i - 1] 开始，到扇区 rounds[i] 结束。举例来说，第 1 阶段从 rounds[0] 开始，到 rounds[1] 结束。

请你以数组形式返回经过次数最多的那几个扇区，按扇区编号升序排列。

注意，赛道按扇区编号升序逆时针形成一个圆（请参见第一个示例）。

示例 1：

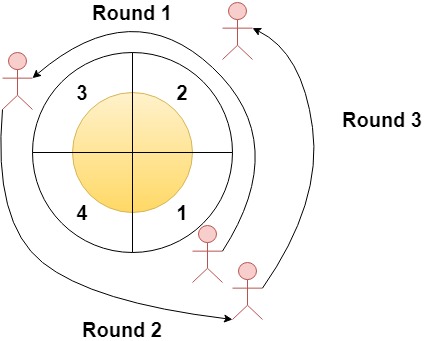
输入：n = 4, rounds = [1,3,1,2]
输出：[1,2]
解释：本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示：
1 –> 2 –> 3（阶段 1 结束）–> 4 –> 1（阶段 2 结束）–> 2（阶段 3 结束，即本场马拉松结束）
其中，扇区 1 和 2 都经过了两次，它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。

示例 2：

输入：n = 2, rounds = [2,1,2,1,2,1,2,1,2]
输出：[2]

示例 3：

输入：n = 7, rounds = [1,3,5,7]
输出：[1,2,3,4,5,6,7]

提示：

2 <= n <= 100
1 <= m <= 100
rounds.length == m + 1
1 <= rounds[i] <= n
rounds[i] != rounds[i + 1] ，其中 0 <= i < m

Metadata

Link: Most Visited Sector in a Circular Track
Difficulty: Easy
Tag: Array Simulation

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The i^th round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

Example 1:

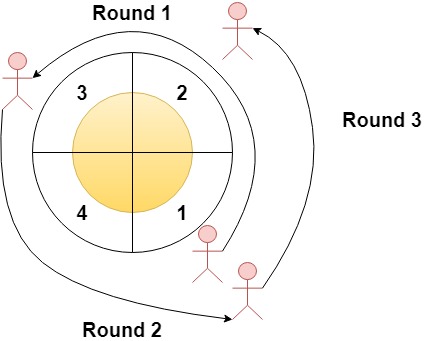
Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 –> 2 –> 3 (end of round 1) –> 4 –> 1 (end of round 2) –> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

Constraints:

2 <= n <= 100
1 <= m <= 100
rounds.length == m + 1
1 <= rounds[i] <= n
rounds[i] != rounds[i + 1] for 0 <= i < m

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;
int cnt[N];

class Solution {
public:
    vector<int> mostVisited(int n, vector<int> &rounds) {
        for (int i = 0; i <= n; ++i) cnt[i] = 0;
        int m = SZ(rounds);
        int i = 1;
        int pos = rounds[0] - 1;
        //	++cnt[pos];
        while (i < m) {
            ++pos;
            ++cnt[pos];
            if (pos == rounds[i])
                ++i;
            //		pt(i, pos);
            if (pos == n)
                pos = 0;
        }
        vector<int> res;
        int Max = 0;
        for (int i = 1; i <= n; ++i) {
            if (cnt[i] == Max) {
                res.push_back(i);
            } else if (cnt[i] > Max) {
                res.clear();
                //	pt(i);
                res.push_back(i);
                Max = cnt[i];
            }
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 你可以获得的最大硬币数目
Difficulty: Medium
Tag: 贪心 数组 数学 博弈 排序

有 3n 堆数目不一的硬币，你和你的朋友们打算按以下方式分硬币：

每一轮中，你将会选出任意 3 堆硬币（不一定连续）。
Alice 将会取走硬币数量最多的那一堆。
你将会取走硬币数量第二多的那一堆。
Bob 将会取走最后一堆。
重复这个过程，直到没有更多硬币。

给你一个整数数组 piles ，其中 piles[i] 是第 i 堆中硬币的数目。

返回你可以获得的最大硬币数目。

示例 1：

输入：piles = [2,4,1,2,7,8]
输出：9
解释：选出 (2, 7, 8) ，Alice 取走 8 枚硬币的那堆，你取走 7 枚硬币的那堆，Bob 取走最后一堆。
选出 (1, 2, 4) , Alice 取走 4 枚硬币的那堆，你取走 2 枚硬币的那堆，Bob 取走最后一堆。
你可以获得的最大硬币数目：7 + 2 = 9.
考虑另外一种情况，如果选出的是 (1, 2, 8) 和 (2, 4, 7) ，你就只能得到 2 + 4 = 6 枚硬币，这不是最优解。

示例 2：

输入：piles = [2,4,5]
输出：4

示例 3：

输入：piles = [9,8,7,6,5,1,2,3,4]
输出：18

提示：

3 <= piles.length <= 10^5
piles.length % 3 == 0
1 <= piles[i] <= 10^4

Metadata

Link: Maximum Number of Coins You Can Get
Difficulty: Medium
Tag: Greedy Array Math Game Theory Sorting

There are 3n piles of coins of varying size, you and your friends will take piles of coins as follows:

In each step, you will choose any 3 piles of coins (not necessarily consecutive).
Of your choice, Alice will pick the pile with the maximum number of coins.
You will pick the next pile with the maximum number of coins.
Your friend Bob will pick the last pile.
Repeat until there are no more piles of coins.

Given an array of integers piles where piles[i] is the number of coins in the i^th pile.

Return the maximum number of coins that you can have.

Example 1:

Input: piles = [2,4,1,2,7,8]
Output: 9
Explanation: Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with 7 coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with 2 coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, 2, 8), (2, 4, 7) you only get 2 + 4 = 6 coins which is not optimal.

Example 2:

Input: piles = [2,4,5]
Output: 4

Example 3:

Input: piles = [9,8,7,6,5,1,2,3,4]
Output: 18

Constraints:

3 <= piles.length <= 10⁵
piles.length % 3 == 0
1 <= piles[i] <= 10⁴

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;

class Solution {
public:
    int maxCoins(vector<int> &piles) {
        int n = SZ(piles);
        sort(all(piles));
        int sz = n / 3;
        int res = 0;
        while (sz--) {
            int a = piles.back();
            piles.pop_back();
            int b = piles.back();
            piles.pop_back();
            res += b;
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 查找大小为 M 的最新分组
Difficulty: Medium
Tag: 数组 二分查找 模拟

给你一个数组 arr ，该数组表示一个从 1 到 n 的数字排列。有一个长度为 n 的二进制字符串，该字符串上的所有位最初都设置为 0 。

在从 1 到 n 的每个步骤 i 中（假设二进制字符串和 arr 都是从 1 开始索引的情况下），二进制字符串上位于位置 arr[i] 的位将会设为 1 。

给你一个整数 m ，请你找出二进制字符串上存在长度为 m 的一组 1 的最后步骤。一组 1 是一个连续的、由 1 组成的子串，且左右两边不再有可以延伸的 1 。

返回存在长度恰好为 m 的 一组 1 的最后步骤。如果不存在这样的步骤，请返回 -1 。

示例 1：

输入：arr = [3,5,1,2,4], m = 1
输出：4
解释：
步骤 1："00100"，由 1 构成的组：["1"]
步骤 2："00101"，由 1 构成的组：["1", "1"]
步骤 3："10101"，由 1 构成的组：["1", "1", "1"]
步骤 4："11101"，由 1 构成的组：["111", "1"]
步骤 5："11111"，由 1 构成的组：["11111"]
存在长度为 1 的一组 1 的最后步骤是步骤 4 。

示例 2：

输入：arr = [3,1,5,4,2], m = 2
输出：-1
解释：
步骤 1："00100"，由 1 构成的组：["1"]
步骤 2："10100"，由 1 构成的组：["1", "1"]
步骤 3："10101"，由 1 构成的组：["1", "1", "1"]
步骤 4："10111"，由 1 构成的组：["1", "111"]
步骤 5："11111"，由 1 构成的组：["11111"]
不管是哪一步骤都无法形成长度为 2 的一组 1 。

示例 3：

输入：arr = [1], m = 1
输出：1

示例 4：

输入：arr = [2,1], m = 2
输出：2

提示：

n == arr.length
1 <= n <= 10^5
1 <= arr[i] <= n
arr 中的所有整数 互不相同
1 <= m <= arr.length

Metadata

Link: Find Latest Group of Size M
Difficulty: Medium
Tag: Array Binary Search Simulation

Given an array arr that represents a permutation of numbers from 1 to n.

You have a binary string of size n that initially has all its bits set to zero. At each step i (assuming both the binary string and arr are 1-indexed) from 1 to n, the bit at position arr[i] is set to 1.

You are also given an integer m. Find the latest step at which there exists a group of ones of length m. A group of ones is a contiguous substring of 1's such that it cannot be extended in either direction.

Return the latest step at which there exists a group of ones of length exactly m. If no such group exists, return -1.

Example 1:

Input: arr = [3,5,1,2,4], m = 1
Output: 4
Explanation: 
Step 1: "00100", groups: ["1"]
Step 2: "00101", groups: ["1", "1"]
Step 3: "10101", groups: ["1", "1", "1"]
Step 4: "11101", groups: ["111", "1"]
Step 5: "11111", groups: ["11111"]
The latest step at which there exists a group of size 1 is step 4.

Example 2:

Input: arr = [3,1,5,4,2], m = 2
Output: -1
Explanation: 
Step 1: "00100", groups: ["1"]
Step 2: "10100", groups: ["1", "1"]
Step 3: "10101", groups: ["1", "1", "1"]
Step 4: "10111", groups: ["1", "111"]
Step 5: "11111", groups: ["11111"]
No group of size 2 exists during any step.

Constraints:

n == arr.length
1 <= m <= n <= 10⁵
1 <= arr[i] <= n
All integers in arr are distinct.

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;
int cnt[N];

class Solution {
public:
    int findLatestStep(vector<int> &arr, int m) {
        set<pII> se;
        int n = SZ(arr);
        for (int i = 0; i <= n; ++i) cnt[i] = 0;
        int res = -1;
        for (int i = 0; i < n; ++i) {
            int x = arr[i];
            if (se.empty()) {
                se.insert(pII(x, x));
                ++cnt[1];
            } else {
                auto pos = se.lower_bound(pII(x, x));
                auto pre = prev(pos);
                int l = x, r = x;
                if (pre != se.end() && pre->se == x - 1) {
                    --cnt[pre->se - pre->fi + 1];
                    l = pre->fi;
                    se.erase(pre);
                }
                if (pos != se.end() && pos->fi == x + 1) {
                    --cnt[pos->se - pos->fi + 1];
                    r = pos->se;
                    se.erase(pos);
                }
                ++cnt[r - l + 1];
                se.insert(pII(l, r));
            }
            if (cnt[m])
                res = i + 1;
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 石子游戏 V
Difficulty: Hard
Tag: 数组 数学 动态规划 博弈

几块石子 排成一行 ，每块石子都有一个关联值，关联值为整数，由数组 stoneValue 给出。

游戏中的每一轮：Alice 会将这行石子分成两个 非空行（即，左侧行和右侧行）；Bob 负责计算每一行的值，即此行中所有石子的值的总和。Bob 会丢弃值最大的行，Alice 的得分为剩下那行的值（每轮累加）。如果两行的值相等，Bob 让 Alice 决定丢弃哪一行。下一轮从剩下的那一行开始。

只 剩下一块石子 时，游戏结束。Alice 的分数最初为 0 。

返回 Alice 能够获得的最大分数 。

示例 1：

输入：stoneValue = [6,2,3,4,5,5]
输出：18
解释：在第一轮中，Alice 将行划分为 [6，2，3]，[4，5，5] 。左行的值是 11 ，右行的值是 14 。Bob 丢弃了右行，Alice 的分数现在是 11 。
在第二轮中，Alice 将行分成 [6]，[2，3] 。这一次 Bob 扔掉了左行，Alice 的分数变成了 16（11 + 5）。
最后一轮 Alice 只能将行分成 [2]，[3] 。Bob 扔掉右行，Alice 的分数现在是 18（16 + 2）。游戏结束，因为这行只剩下一块石头了。

示例 2：

输入：stoneValue = [7,7,7,7,7,7,7]
输出：28

示例 3：

输入：stoneValue = [4]
输出：0

提示：

1 <= stoneValue.length <= 500
1 <= stoneValue[i] <= 10^6

Metadata

Link: Stone Game V
Difficulty: Hard
Tag: Array Math Dynamic Programming Game Theory

There are several stones arranged in a row, and each stone has an associated value which is an integer given in the array stoneValue.

In each round of the game, Alice divides the row into two non-empty rows (i.e. left row and right row), then Bob calculates the value of each row which is the sum of the values of all the stones in this row. Bob throws away the row which has the maximum value, and Alice's score increases by the value of the remaining row. If the value of the two rows are equal, Bob lets Alice decide which row will be thrown away. The next round starts with the remaining row.

The game ends when there is only one stone remaining. Alice's is initially zero.

Return the maximum score that Alice can obtain.

Example 1:

Input: stoneValue = [6,2,3,4,5,5]
Output: 18
Explanation: In the first round, Alice divides the row to [6,2,3], [4,5,5]. The left row has the value 11 and the right row has value 14. Bob throws away the right row and Alice's score is now 11.
In the second round Alice divides the row to [6], [2,3]. This time Bob throws away the left row and Alice's score becomes 16 (11 + 5).
The last round Alice has only one choice to divide the row which is [2], [3]. Bob throws away the right row and Alice's score is now 18 (16 + 2). The game ends because only one stone is remaining in the row.

Example 2:

Input: stoneValue = [7,7,7,7,7,7,7]
Output: 28

Example 3:

Input: stoneValue = [4]
Output: 0

Constraints:

1 <= stoneValue.length <= 500
1 <= stoneValue[i] <= 10⁶

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 5e2 + 10;
// int n;
int a[N], sum[N], f[N][N];

int dfs(int l, int r) {
    if (l >= r)
        return 0;
    if (f[l][r] != -1)
        return f[l][r];
    int tot = sum[r] - sum[l - 1];
    int now = 0;
    int Max = 0;
    for (int i = l; i <= r; ++i) {
        now += a[i];
        int oth = tot - now;
        if (now < oth) {
            chmax(Max, dfs(l, i) + now);
        } else if (now == oth) {
            chmax(Max, dfs(l, i) + now);
            chmax(Max, dfs(i + 1, r) + oth);
        } else {
            chmax(Max, dfs(i + 1, r) + oth);
        }
    }
    return f[l][r] = Max;
}

class Solution {
public:
    int stoneGameV(vector<int> &stoneValue) {
        int n = SZ(stoneValue);
        for (int i = 0; i < n; ++i) {
            a[i + 1] = stoneValue[i];
            sum[i + 1] = sum[i] + a[i + 1];
        }
        memset(f, -1, sizeof f);
        return dfs(1, n);
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023