biweekly-contest-91
A
Statement
Metadata
- Link: 不同的平均值数目
- Difficulty: Easy
- Tag:
给你一个下标从 0 开始长度为 偶数 的整数数组 nums 。
只要 nums 不是 空数组,你就重复执行以下步骤:
- 找到
nums中的最小值,并删除它。 - 找到
nums中的最大值,并删除它。 - 计算删除两数的平均值。
两数 a 和 b 的 平均值 为 (a + b) / 2 。
- 比方说,
2和3的平均值是(2 + 3) / 2 = 2.5。
返回上述过程能得到的 不同 平均值的数目。
注意 ,如果最小值或者最大值有重复元素,可以删除任意一个。
示例 1:
输入:nums = [4,1,4,0,3,5]
输出:2
解释:
1. 删除 0 和 5 ,平均值是 (0 + 5) / 2 = 2.5 ,现在 nums = [4,1,4,3] 。
2. 删除 1 和 4 ,平均值是 (1 + 4) / 2 = 2.5 ,现在 nums = [4,3] 。
3. 删除 3 和 4 ,平均值是 (3 + 4) / 2 = 3.5 。
2.5 ,2.5 和 3.5 之中总共有 2 个不同的数,我们返回 2 。
示例 2:
输入:nums = [1,100]
输出:1
解释:
删除 1 和 100 后只有一个平均值,所以我们返回 1 。
提示:
2 <= nums.length <= 100nums.length是偶数。0 <= nums[i] <= 100
Metadata
- Link: Number of Distinct Averages
- Difficulty: Easy
- Tag:
You are given a 0-indexed integer array nums of even length.
As long as nums is not empty, you must repetitively:
- Find the minimum number in
numsand remove it. - Find the maximum number in
numsand remove it. - Calculate the average of the two removed numbers.
The average of two numbers a and b is (a + b) / 2.
- For example, the average of
2and3is(2 + 3) / 2 = 2.5.
Return the number of distinct averages calculated using the above process.
Note that when there is a tie for a minimum or maximum number, any can be removed.
Example 1:
Input: nums = [4,1,4,0,3,5]
Output: 2
Explanation:
1. Remove 0 and 5, and the average is (0 + 5) / 2 = 2.5. Now, nums = [4,1,4,3].
2. Remove 1 and 4. The average is (1 + 4) / 2 = 2.5, and nums = [4,3].
3. Remove 3 and 4, and the average is (3 + 4) / 2 = 3.5.
Since there are 2 distinct numbers among 2.5, 2.5, and 3.5, we return 2.
Example 2:
Input: nums = [1,100]
Output: 1
Explanation:
There is only one average to be calculated after removing 1 and 100, so we return 1.
Constraints:
2 <= nums.length <= 100nums.lengthis even.0 <= nums[i] <= 100
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int distinctAverages(vector<int> &nums) {
int n = int(nums.size());
sort(all(nums));
set<int> se;
int l = 0;
int r = n - 1;
while (l < r) {
se.insert(nums[l] + nums[r]);
++l;
--r;
}
return int(se.size());
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 统计构造好字符串的方案数
- Difficulty: Medium
- Tag:
给你整数 zero ,one ,low 和 high ,我们从空字符串开始构造一个字符串,每一步执行下面操作中的一种:
- 将
'0'在字符串末尾添加zero次。 - 将
'1'在字符串末尾添加one次。
以上操作可以执行任意次。
如果通过以上过程得到一个 长度 在 low 和 high 之间(包含上下边界)的字符串,那么这个字符串我们称为 好 字符串。
请你返回满足以上要求的 不同 好字符串数目。由于答案可能很大,请将结果对 109 + 7 取余 后返回。
示例 1:
输入:low = 3, high = 3, zero = 1, one = 1
输出:8
解释:
一个可能的好字符串是 "011" 。
可以这样构造得到:"" -> "0" -> "01" -> "011" 。
从 "000" 到 "111" 之间所有的二进制字符串都是好字符串。
示例 2:
输入:low = 2, high = 3, zero = 1, one = 2
输出:5
解释:好字符串为 "00" ,"11" ,"000" ,"110" 和 "011" 。
提示:
1 <= low <= high <= 1051 <= zero, one <= low
Metadata
- Link: Count Ways To Build Good Strings
- Difficulty: Medium
- Tag:
Given the integers zero, one, low, and high, we can construct a string by starting with an empty string, and then at each step perform either of the following:
- Append the character
'0'zerotimes. - Append the character
'1'onetimes.
This can be performed any number of times.
A good string is a string constructed by the above process having a length between low and high (inclusive).
Return the number of different good strings that can be constructed satisfying these properties. Since the answer can be large, return it modulo 109 + 7.
Example 1:
Input: low = 3, high = 3, zero = 1, one = 1
Output: 8
Explanation:
One possible valid good string is "011".
It can be constructed as follows: "" -> "0" -> "01" -> "011".
All binary strings from "000" to "111" are good strings in this example.
Example 2:
Input: low = 2, high = 3, zero = 1, one = 2
Output: 5
Explanation: The good strings are "00", "11", "000", "110", and "011".
Constraints:
1 <= low <= high <= 1051 <= zero, one <= low
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
constexpr int mod = 1e9 + 7;
class Solution {
public:
int countGoodStrings(int low, int high, int zero, int one) {
auto f = vector<int>(high + 10, 0);
f[0] = 1;
for (int i = 1; i <= high; i++) {
if (i - zero >= 0) {
f[i] = (f[i] + f[i - zero]) % mod;
}
if (i - one >= 0) {
f[i] = (f[i] + f[i - one]) % mod;
}
}
int res = 0;
for (int i = low; i <= high; i++) {
res += f[i];
res %= mod;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 树上最大得分和路径
- Difficulty: Medium
- Tag:
一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
- 一开始,Alice 在节点
0处,Bob 在节点bob处。 - 每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。 - 对于他们之间路径上的 每一个 节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
- 如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
示例 1:
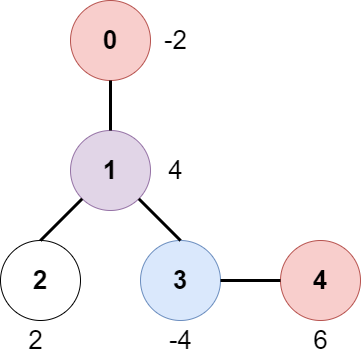
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
输出:6
解释:
上图展示了输入给出的一棵树。游戏进行如下:
- Alice 一开始在节点 0 处,Bob 在节点 3 处。他们分别打开所在节点的门。
Alice 得分为 -2 。
- Alice 和 Bob 都移动到节点 1 。
因为他们同时到达这个节点,他们一起打开门并平分得分。
Alice 的得分变为 -2 + (4 / 2) = 0 。
- Alice 移动到节点 3 。因为 Bob 已经打开了这扇门,Alice 得分不变。
Bob 移动到节点 0 ,并停止移动。
- Alice 移动到节点 4 并打开这个节点的门,她得分变为 0 + 6 = 6 。
现在,Alice 和 Bob 都不能进行任何移动了,所以游戏结束。
Alice 无法得到更高分数。
示例 2:

输入:edges = [[0,1]], bob = 1, amount = [-7280,2350]
输出:-7280
解释:
Alice 按照路径 0->1 移动,同时 Bob 按照路径 1->0 移动。
所以 Alice 只打开节点 0 处的门,她的得分为 -7280 。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-104, 104]之间的一个 偶数 。
Metadata
- Link: Most Profitable Path in a Tree
- Difficulty: Medium
- Tag:
There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:
- the price needed to open the gate at node
i, ifamount[i]is negative, or, - the cash reward obtained on opening the gate at node
i, otherwise.
The game goes on as follows:
- Initially, Alice is at node
0and Bob is at nodebob. - At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node
0. - For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
- If the gate is already open, no price will be required, nor will there be any cash reward.
- If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is
c, then both Alice and Bob payc / 2each. Similarly, if the reward at the gate isc, both of them receivec / 2each.
- If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node
0, he stops moving. Note that these events are independent of each other.
Return the maximum net income Alice can have if she travels towards the optimal leaf node.
Example 1:

Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
Output: 6
Explanation:
The above diagram represents the given tree. The game goes as follows:
- Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
Alice's net income is now -2.
- Both Alice and Bob move to node 1.
Since they reach here simultaneously, they open the gate together and share the reward.
Alice's net income becomes -2 + (4 / 2) = 0.
- Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
Bob moves on to node 0, and stops moving.
- Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
Now, neither Alice nor Bob can make any further moves, and the game ends.
It is not possible for Alice to get a higher net income.
Example 2:

Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
Output: -7280
Explanation:
Alice follows the path 0->1 whereas Bob follows the path 1->0.
Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.
Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.1 <= bob < namount.length == namount[i]is an even integer in the range[-104, 104].
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 2e5 + 10, M = 20;
const int INF = 0x3f3f3f3f;
struct Graph {
struct E {
int to, nx, w;
} e[N << 1];
int h[N], cnt;
void init(int n) {
for (int i = 0; i <= n; ++i) h[i] = -1;
cnt = -1;
}
void addedge(int u, int v, int w = 0) {
e[++cnt] = {v, h[u], w};
h[u] = cnt;
}
} G;
struct LCA {
int fa[N][M], dis[N][M];
int deep[N];
void bfs(int rt) {
queue<int> q;
deep[rt] = 0;
fa[rt][0] = rt;
dis[rt][0] = 0;
q.emplace(rt);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 1; i < M; ++i) {
dis[u][i] = dis[u][i - 1] + dis[fa[u][i - 1]][i - 1];
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for (int i = G.h[u]; ~i; i = G.e[i].nx) {
int v = G.e[i].to, w = G.e[i].w;
if (v == fa[u][0])
continue;
deep[v] = deep[u] + 1;
fa[v][0] = u;
dis[v][0] = w;
q.emplace(v);
}
}
}
void init(int rt) {
bfs(rt);
}
int querylca(int u, int v) {
if (deep[u] > deep[v])
swap(u, v);
for (int det = deep[v] - deep[u], i = 0; det; det >>= 1, ++i) {
if (det & 1)
v = fa[v][i];
}
if (u == v)
return u;
for (int i = M - 1; i >= 0; --i) {
if (fa[u][i] == fa[v][i])
continue;
u = fa[u][i];
v = fa[v][i];
}
return fa[u][0];
}
} lca;
class Solution {
public:
int fa[N], dep[N], sum[N], f[N];
vector<int> amount;
vector<int> leaf_node;
void dfs(int rt, int deep) {
dep[rt] = deep;
sum[rt] = amount[rt - 1] + sum[fa[rt]];
int cnt = 0;
for (int i = G.h[rt]; ~i; i = G.e[i].nx) {
int v = G.e[i].to;
if (v == fa[rt]) {
continue;
}
fa[v] = rt;
dfs(v, deep + 1);
++cnt;
}
if (cnt == 0) {
leaf_node.push_back(rt);
}
}
int mostProfitablePath(vector<vector<int>> &edges, int bob, vector<int> &amount) {
int n = int(amount.size());
this->amount = amount;
leaf_node.clear();
G.init(n);
for (int i = 0; i <= n; i++) {
fa[i] = 0;
dep[i] = 0;
sum[i] = 0;
f[i] = 0;
}
++bob;
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
++u, ++v;
G.addedge(u, v);
G.addedge(v, u);
}
lca.init(1);
dfs(1, 0);
{
int u = bob;
int base_deep = dep[u];
vector<int> key_node;
while (u != 0) {
key_node.push_back(u);
int gap = base_deep - dep[u];
if (dep[u] < gap) {
f[u] = amount[u - 1];
} else if (dep[u] == gap) {
f[u] = amount[u - 1] / 2;
} else {
f[u] = 0;
}
u = fa[u];
}
reverse(all(key_node));
for (size_t i = 1; i < key_node.size(); i++) {
f[key_node[i]] += f[key_node[i - 1]];
}
}
int res = -INF;
for (const auto &u : leaf_node) {
int _lca = lca.querylca(u, bob);
int cur_sum = 0;
cur_sum += sum[u] - sum[_lca] + f[_lca];
res = max(res, cur_sum);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 根据限制分割消息
- Difficulty: Hard
- Tag:
给你一个字符串 message 和一个正整数 limit 。
你需要根据 limit 将 message 分割 成一个或多个 部分 。每个部分的结尾都是 "<a/b>" ,其中 "b" 用分割出来的总数 替换, "a" 用当前部分所在的编号 替换 ,编号从 1 到 b 依次编号。除此以外,除了最后一部分长度 小于等于 limit 以外,其他每一部分(包括结尾部分)的长度都应该 等于 limit 。
你需要确保分割后的结果数组,删掉每部分的结尾并 按顺序 连起来后,能够得到 message 。同时,结果数组越短越好。
请你返回 message 分割后得到的结果数组。如果无法按要求分割 message ,返回一个空数组。
示例 1:
输入:message = "this is really a very awesome message", limit = 9
输出:["thi<1/14>","s i<2/14>","s r<3/14>","eal<4/14>","ly <5/14>","a v<6/14>","ery<7/14>"," aw<8/14>","eso<9/14>","me<10/14>"," m<11/14>","es<12/14>","sa<13/14>","ge<14/14>"]
解释:
前面 9 个部分分别从 message 中得到 3 个字符。
接下来的 5 个部分分别从 message 中得到 2 个字符。
这个例子中,包含最后一个部分在内,每个部分的长度都为 9 。
可以证明没有办法分割成少于 14 个部分。
示例 2:
输入:message = "short message", limit = 15
输出:["short mess<½>","age<2/2>"]
解释:
在给定限制下,字符串可以分成两个部分:
- 第一个部分包含 10 个字符,长度为 15 。
- 第二个部分包含 3 个字符,长度为 8 。
提示:
1 <= message.length <= 104message只包含小写英文字母和' '。1 <= limit <= 104
Metadata
- Link: Split Message Based on Limit
- Difficulty: Hard
- Tag:
You are given a string, message, and a positive integer, limit.
You must split message into one or more parts based on limit. Each resulting part should have the suffix "<a/b>", where "b" is to be replaced with the total number of parts and "a" is to be replaced with the index of the part, starting from 1 and going up to b. Additionally, the length of each resulting part (including its suffix) should be equal to limit, except for the last part whose length can be at most limit.
The resulting parts should be formed such that when their suffixes are removed and they are all concatenated in order, they should be equal to message. Also, the result should contain as few parts as possible.
Return the parts message would be split into as an array of strings. If it is impossible to split message as required, return an empty array.
Example 1:
Input: message = "this is really a very awesome message", limit = 9
Output: ["thi<1/14>","s i<2/14>","s r<3/14>","eal<4/14>","ly <5/14>","a v<6/14>","ery<7/14>"," aw<8/14>","eso<9/14>","me<10/14>"," m<11/14>","es<12/14>","sa<13/14>","ge<14/14>"]
Explanation:
The first 9 parts take 3 characters each from the beginning of message.
The next 5 parts take 2 characters each to finish splitting message.
In this example, each part, including the last, has length 9.
It can be shown it is not possible to split message into less than 14 parts.
Example 2:
Input: message = "short message", limit = 15
Output: ["short mess<½>","age<2/2>"]
Explanation:
Under the given constraints, the string can be split into two parts:
- The first part comprises of the first 10 characters, and has a length 15.
- The next part comprises of the last 3 characters, and has a length 8.
Constraints:
1 <= message.length <= 104messageconsists only of lowercase English letters and' '.1 <= limit <= 104
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 1e4 + 10;
class Solution {
public:
bool has_init = false;
int f[N], g[N];
void init() {
f[0] = 0;
for (int i = 1; i < N; i++) {
int len = int(to_string(i).size());
f[i] = f[i - 1] + len;
g[i] = f[i] + (3 + len) * i;
}
}
vector<string> splitMessage(string message, int limit) {
if (has_init == false) {
init();
has_init = true;
}
int n = int(message.size());
int res = -1;
for (int i = max(1, n / limit); i < N; i++) {
int high = limit * i - g[i];
int low = (limit * (i - 1)) - g[i] + (int(to_string(i).size()) * 2 + 3);
// cout << i << " " << low << " " << high << endl;
if (n >= low && n <= high) {
res = i;
break;
}
}
if (res == -1) {
return vector<string>();
}
{
reverse(all(message));
auto ans = vector<string>();
for (int i = 1; i <= res; i++) {
string tmp = "<";
tmp += to_string(i);
tmp += "/";
tmp += to_string(res);
tmp += ">";
string ttmp = "";
int remind = int(limit - tmp.size());
while (!message.empty() && remind) {
--remind;
ttmp += message.back();
message.pop_back();
}
ttmp += tmp;
ans.push_back(ttmp);
}
return ans;
}
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif