weekly-contest-290
A
Statement
Metadata
- Link: 多个数组求交集
- Difficulty: Easy
- Tag:
给你一个二维整数数组 nums ,其中 nums[i] 是由 不同 正整数组成的一个非空数组,按 升序排列 返回一个数组,数组中的每个元素在 nums 所有数组 中都出现过。
示例 1:
输入:nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]]
输出:[3,4]
解释:
nums[0] = [3,1,2,4,5],nums[1] = [1,2,3,4],nums[2] = [3,4,5,6],在 nums 中每个数组中都出现的数字是 3 和 4 ,所以返回 [3,4] 。示例 2:
输入:nums = [[1,2,3],[4,5,6]]
输出:[]
解释:
不存在同时出现在 nums[0] 和 nums[1] 的整数,所以返回一个空列表 [] 。
提示:
1 <= nums.length <= 10001 <= sum(nums[i].length) <= 10001 <= nums[i][j] <= 1000nums[i]中的所有值 互不相同
Metadata
- Link: Intersection of Multiple Arrays
- Difficulty: Easy
- Tag:
Given a 2D integer array nums where nums[i] is a non-empty array of distinct positive integers, return the list of integers that are present in each array of nums sorted in ascending order.
Example 1:
Input: nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]]
Output: [3,4]
Explanation:
The only integers present in each of nums[0] = [3,1,2,4,5], nums[1] = [1,2,3,4], and nums[2] = [3,4,5,6] are 3 and 4, so we return [3,4].Example 2:
Input: nums = [[1,2,3],[4,5,6]]
Output: []
Explanation:
There does not exist any integer present both in nums[0] and nums[1], so we return an empty list [].
Constraints:
1 <= nums.length <= 10001 <= sum(nums[i].length) <= 10001 <= nums[i][j] <= 1000- All the values of
nums[i]are unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> intersection(vector<vector<int>> &nums) {
int n = nums.size();
map<int, int> mp;
for (const auto &v : nums) {
for (const auto &a : v) {
mp[a]++;
}
}
auto res = vector<int>();
for (const auto &[k, v] : mp) {
if (v == n) {
res.push_back(k);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 统计圆内格点数目
- Difficulty: Medium
- Tag:
给你一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆,返回出现在 至少一个 圆内的 格点数目 。
注意:
- 格点 是指整数坐标对应的点。
- 圆周上的点 也被视为出现在圆内的点。
示例 1:
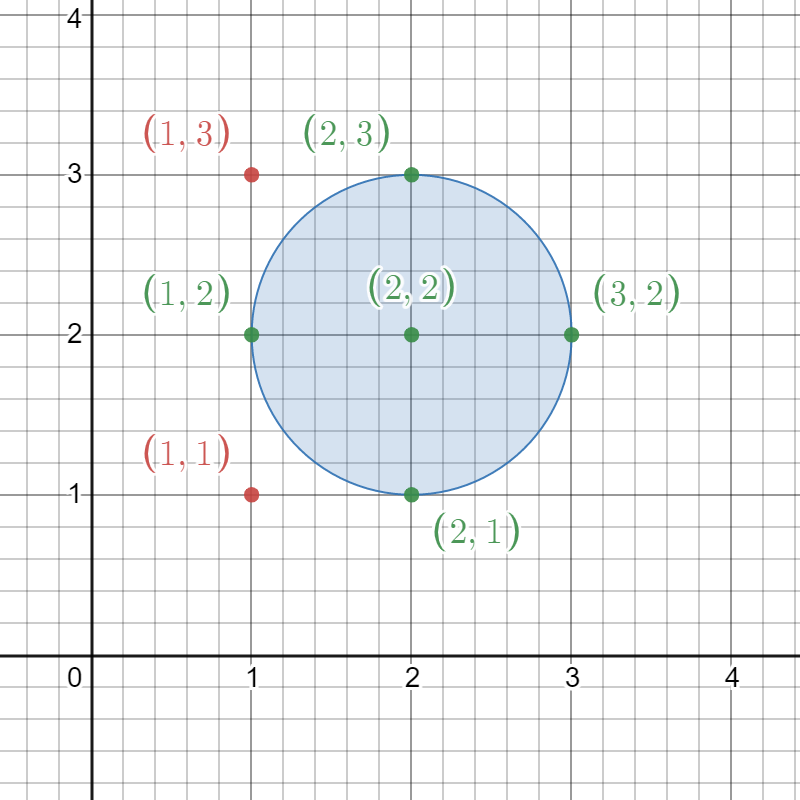
输入:circles = [[2,2,1]]
输出:5
解释:
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2),在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点,并未出现在圆内。
因此,出现在至少一个圆内的格点数目是 5 。示例 2:
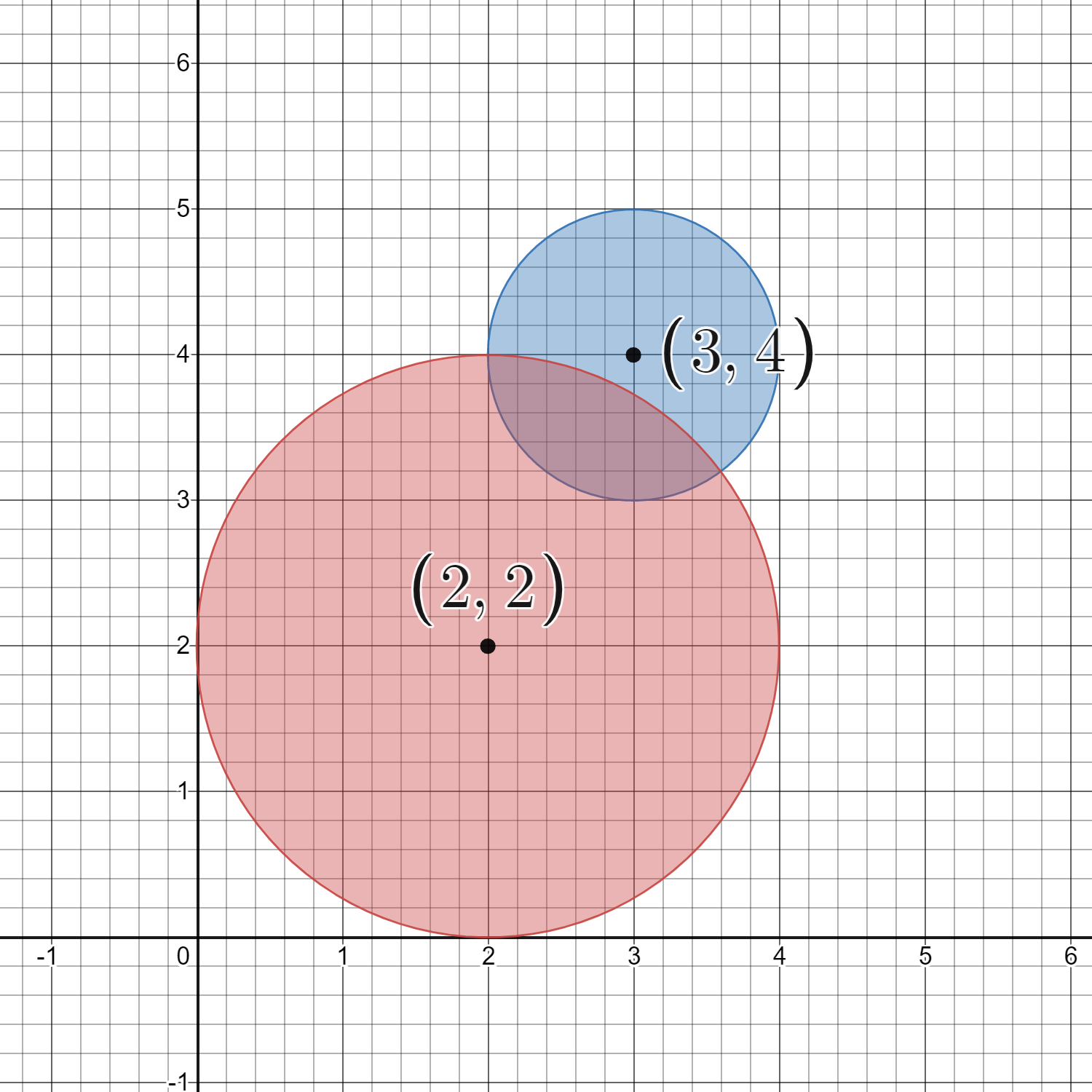
输入:circles = [[2,2,2],[3,4,1]]
输出:16
解释:
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。
提示:
1 <= circles.length <= 200circles[i].length == 31 <= xi, yi <= 1001 <= ri <= min(xi, yi)
Metadata
- Link: Count Lattice Points Inside a Circle
- Difficulty: Medium
- Tag:
Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return the number of lattice points that are present inside at least one circle.
Note:
- A lattice point is a point with integer coordinates.
- Points that lie on the circumference of a circle are also considered to be inside it.
Example 1:

Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.Example 2:

Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
Constraints:
1 <= circles.length <= 200circles[i].length == 31 <= xi, yi <= 1001 <= ri <= min(xi, yi)
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int countLatticePoints(vector<vector<int>> &circles) {
const auto ok = [&](int x, int y) {
for (const auto &c : circles) {
int cx = c[0];
int cy = c[1];
int r = c[2];
int xx = (x - cx);
int yy = (y - cy);
if (xx * xx + yy * yy <= r * r) {
return true;
}
}
return false;
};
int res = 0;
for (int i = -200; i <= 200; i++) {
for (int j = -200; j <= 200; j++) {
if (ok(i, j)) {
++res;
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 统计包含每个点的矩形数目
- Difficulty: Medium
- Tag:
给你一个二维整数数组 rectangles ,其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ,其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。
第 i 个矩形的 左下角 在 (0, 0) 处,右上角 在 (li, hi) 。
请你返回一个整数数组 count ,长度为 points.length,其中 count[j]是 包含 第 j 个点的矩形数目。
如果 0 <= xj <= li 且 0 <= yj <= hi ,那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ,这个点也被视为被矩形包含。
示例 1:
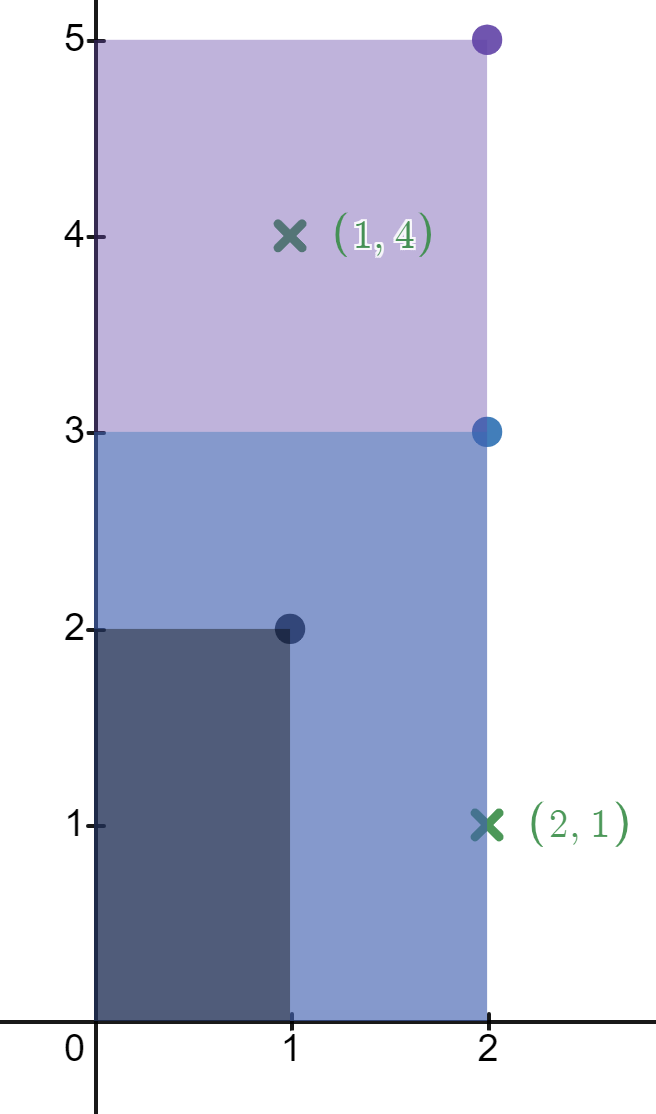
输入:rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
输出:[2,1]
解释:
第一个矩形不包含任何点。
第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以,我们返回 [2, 1] 。
示例 2:
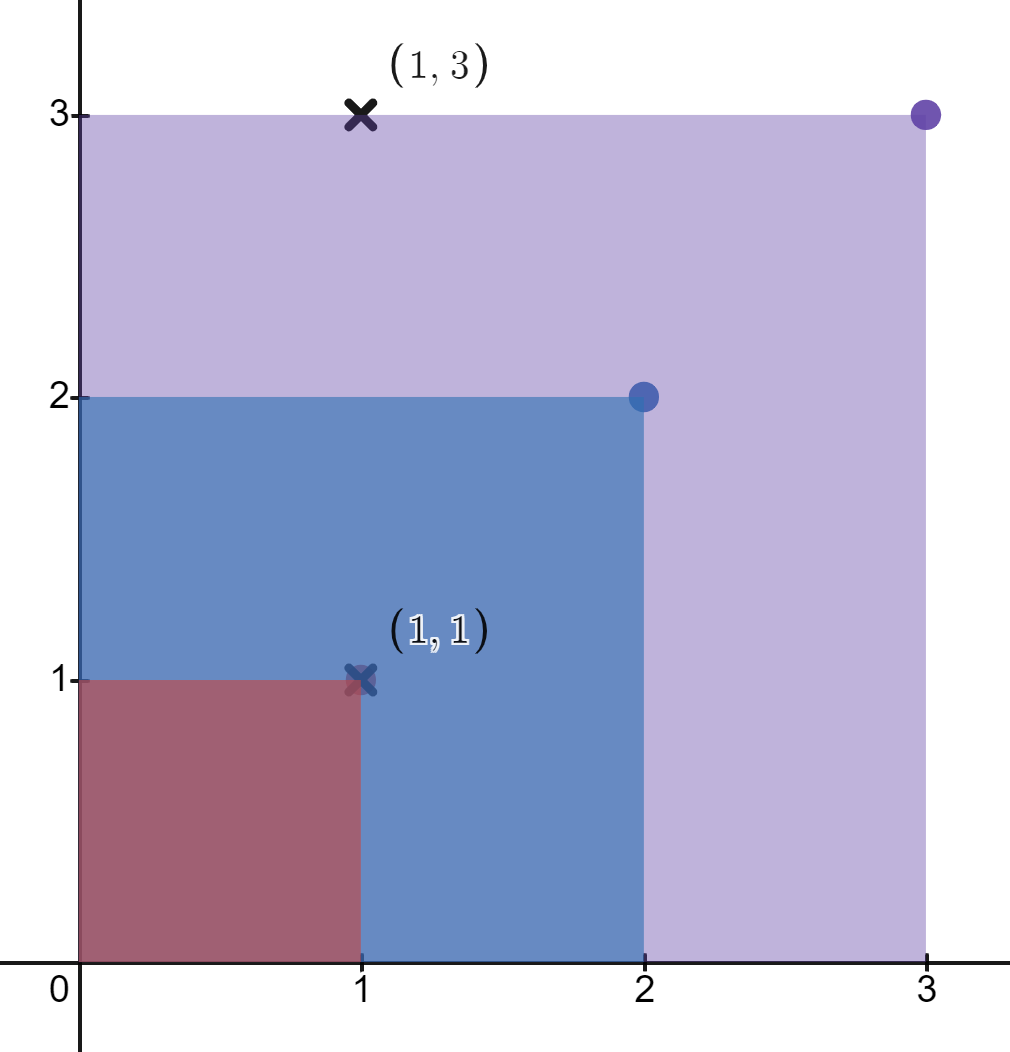
输入:rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
输出:[1,3]
解释:
第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以,我们返回 [1, 3] 。
提示:
1 <= rectangles.length, points.length <= 5 * 104rectangles[i].length == points[j].length == 21 <= li, xj <= 1091 <= hi, yj <= 100- 所有
rectangles互不相同 。 - 所有
points互不相同 。
Metadata
- Link: Count Number of Rectangles Containing Each Point
- Difficulty: Medium
- Tag:
You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).
The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).
Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jth point.
The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.
Example 1:

Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
Output: [2,1]
Explanation:
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return [2, 1].
Example 2:

Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
Output: [1,3]
Explanation:
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return [1, 3].
Constraints:
1 <= rectangles.length, points.length <= 5 * 104rectangles[i].length == points[j].length == 21 <= li, xj <= 1091 <= hi, yj <= 100- All the
rectanglesare unique. - All the
pointsare unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct R {
int l, h, ix;
bool operator<(const R& other) const {
if (l == other.l) {
return h < other.h;
}
return l < other.l;
}
};
const int N = 1e5 + 10;
struct BIT {
int a[N];
int n;
void init(int n) {
this->n = n;
memset(a, 0, sizeof(a[0]) * (n + 5));
}
int lowbit(int x) {
return x & -x;
}
void add(int x, ll v) {
for (int i = x; i < n; i += lowbit(i)) a[i] += v;
}
ll query(int x) {
ll ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) ret += a[i];
return ret;
}
ll query(int l, int r) {
if (l > r)
return 0;
return query(r) - query(l - 1);
}
void add(int l, int r, ll v) {
if (l > r)
return;
add(l, v);
add(r + 1, -v);
}
} bit;
struct Hash {
vector<db> a;
db& operator[](int x) {
return a[x - 1];
}
int size() {
return a.size();
}
void init() {
a.clear();
}
void add(db x) {
a.push_back(x);
}
void gao() {
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
}
int get(db x) {
return lower_bound(a.begin(), a.end(), x) - a.begin() + 1;
}
} hl, hh;
class Solution {
public:
vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
int np = points.size();
hl.init();
hh.init();
for (const auto& r : rectangles) {
hl.add(r[0]);
hh.add(r[1]);
}
for (const auto& p : points) {
hl.add(p[0]);
hh.add(p[1]);
}
hl.gao();
hh.gao();
auto vr = vector<vector<R>>(hl.size() + 1, vector<R>());
for (const auto& r : rectangles) {
int l = hl.get(r[0]);
int h = hh.get(r[1]);
vr[l].push_back({
.l = l,
.h = h,
.ix = 0,
});
}
int ix = 0;
auto vp = vector<vector<R>>(hl.size() + 1, vector<R>());
for (const auto& p : points) {
int l = hl.get(p[0]);
int h = hh.get(p[1]);
vp[l].push_back({
.l = l,
.h = h,
.ix = ix,
});
ix++;
}
auto res = vector<int>(np, 0);
bit.init(hh.size() + 5);
for (int i = hl.size(); i >= 1; i--) {
for (const auto& r : vr[i]) {
bit.add(r.h, 1);
}
for (const auto& p : vp[i]) {
res[p.ix] = bit.query(p.h, hh.size());
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 花期内花的数目
- Difficulty: Hard
- Tag:
给你一个下标从 0 开始的二维整数数组 flowers ,其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi (都 包含)。同时给你一个下标从 0 开始大小为 n 的整数数组 persons ,persons[i] 是第 i 个人来看花的时间。
请你返回一个大小为 n 的整数数组 answer ,其中 answer[i]是第 i 个人到达时在花期内花的 数目 。
示例 1:
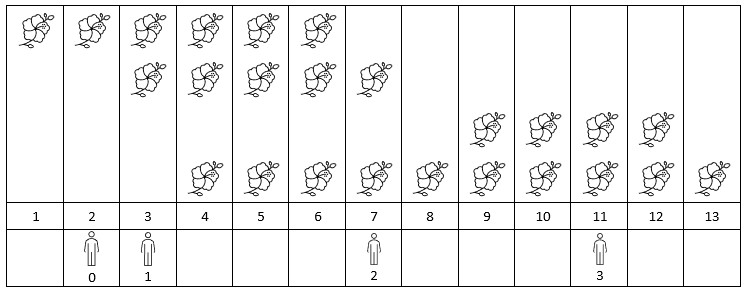
输入:flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
输出:[1,2,2,2]
解释:上图展示了每朵花的花期时间,和每个人的到达时间。
对每个人,我们返回他们到达时在花期内花的数目。
示例 2:
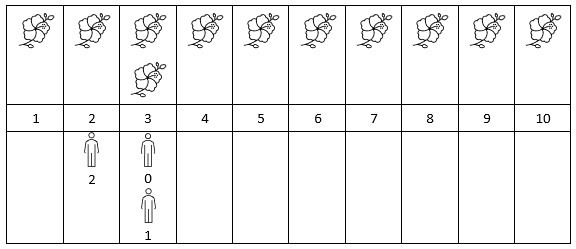
输入:flowers = [[1,10],[3,3]], persons = [3,3,2]
输出:[2,2,1]
解释:上图展示了每朵花的花期时间,和每个人的到达时间。
对每个人,我们返回他们到达时在花期内花的数目。
提示:
1 <= flowers.length <= 5 * 104flowers[i].length == 21 <= starti <= endi <= 1091 <= persons.length <= 5 * 1041 <= persons[i] <= 109
Metadata
- Link: Number of Flowers in Full Bloom
- Difficulty: Hard
- Tag:
You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array persons of size n, where persons[i] is the time that the ith person will arrive to see the flowers.
Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.
Example 1:

Input: flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Example 2:

Input: flowers = [[1,10],[3,3]], persons = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Constraints:
1 <= flowers.length <= 5 * 104flowers[i].length == 21 <= starti <= endi <= 1091 <= persons.length <= 5 * 1041 <= persons[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 2e5 + 10;
struct BIT {
int a[N];
int n;
void init(int n) {
this->n = n;
memset(a, 0, sizeof(a[0]) * (n + 5));
}
int lowbit(int x) {
return x & -x;
}
void add(int x, ll v) {
for (int i = x; i < n; i += lowbit(i)) a[i] += v;
}
ll query(int x) {
ll ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) ret += a[i];
return ret;
}
ll query(int l, int r) {
if (l > r)
return 0;
return query(r) - query(l - 1);
}
void add(int l, int r, ll v) {
if (l > r)
return;
add(l, v);
add(r + 1, -v);
}
} bit;
struct Hash {
vector<db> a;
db& operator[](int x) {
return a[x - 1];
}
int size() {
return a.size();
}
void init() {
a.clear();
}
void add(db x) {
a.push_back(x);
}
void gao() {
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
}
int get(db x) {
return lower_bound(a.begin(), a.end(), x) - a.begin() + 1;
}
} hs;
class Solution {
public:
vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
hs.init();
for (const auto& f : flowers) {
hs.add(f[0]);
hs.add(f[1]);
}
for (const auto& p : persons) {
hs.add(p);
}
hs.gao();
bit.init(hs.size() + 5);
for (const auto& f : flowers) {
int l = hs.get(f[0]);
int r = hs.get(f[1]);
bit.add(l, r, 1);
}
auto res = vector<int>();
for (const auto& p : persons) {
res.push_back(bit.query(hs.get(p)));
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif