biweekly-contest-82
A
Statement
Metadata
- Link: 计算布尔二叉树的值
- Difficulty: Easy
- Tag:
给你一棵 完整二叉树 的根,这棵树有以下特征:
- 叶子节点 要么值为
0要么值为1,其中0表示False,1表示True。 - 非叶子节点 要么值为
2要么值为3,其中2表示逻辑或OR,3表示逻辑与AND。
计算 一个节点的值方式如下:
- 如果节点是个叶子节点,那么节点的 值 为它本身,即
True或者False。 - 否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:
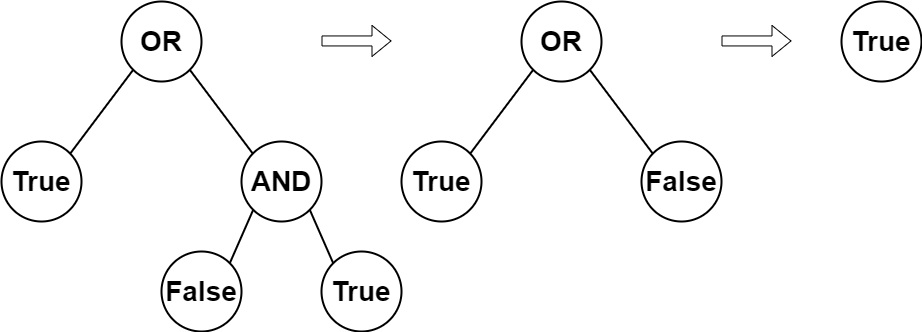
输入:root = [2,1,3,null,null,0,1]
输出:true
解释:上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。示例 2:
输入:root = [0]
输出:false
解释:根节点是叶子节点,且值为 false,所以我们返回 false 。
提示:
- 树中节点数目在
[1, 1000]之间。 0 <= Node.val <= 3- 每个节点的孩子数为
0或2。 - 叶子节点的值为
0或1。 - 非叶子节点的值为
2或3。
Metadata
- Link: Evaluate Boolean Binary Tree
- Difficulty: Easy
- Tag:
You are given the root of a full binary tree with the following properties:
- Leaf nodes have either the value
0or1, where0representsFalseand1representsTrue. - Non-leaf nodes have either the value
2or3, where2represents the booleanORand3represents the booleanAND.
The evaluation of a node is as follows:
- If the node is a leaf node, the evaluation is the value of the node, i.e.
TrueorFalse. - Otherwise, evaluate the node's two children and apply the boolean operation of its value with the children's evaluations.
Return the boolean result of evaluating the root node.
A full binary tree is a binary tree where each node has either 0 or 2 children.
A leaf node is a node that has zero children.
Example 1:

Input: root = [2,1,3,null,null,0,1]
Output: true
Explanation: The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.Example 2:
Input: root = [0]
Output: false
Explanation: The root node is a leaf node and it evaluates to false, so we return false.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 3- Every node has either
0or2children. - Leaf nodes have a value of
0or1. - Non-leaf nodes have a value of
2or3.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#ifdef LOCAL
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
#endif
class Solution {
public:
bool dfs(TreeNode *root) {
if (!root->left && !root->right) {
return root->val;
}
if (root->val == 2) {
return dfs(root->left) || dfs(root->right);
}
return dfs(root->left) && dfs(root->right);
}
bool evaluateTree(TreeNode *root) {
return dfs(root);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 坐上公交的最晚时间
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始长度为 n 的整数数组 buses ,其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ,其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同,所有乘客到达的时间也互不相同。
给你一个整数 capacity ,表示每辆公交车 最多 能容纳的乘客数目。
每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达,公交在 x 时刻出发,满足 y <= x 且公交没有满,那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。
返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
注意:数组 buses 和 passengers 不一定是有序的。
示例 1:
输入:buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出:16
解释:
第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达,所以你必须在第二位乘客之前到达。示例 2:
输入:buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
输出:20
解释:
第 1 辆公交车载着第 4 位乘客。
第 2 辆公交车载着第 6 位和第 2 位乘客。
第 3 辆公交车载着第 1 位乘客和你。
提示:
n == buses.lengthm == passengers.length1 <= n, m, capacity <= 1052 <= buses[i], passengers[i] <= 109buses中的元素 互不相同 。passengers中的元素 互不相同 。
Metadata
- Link: The Latest Time to Catch a Bus
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array buses of length n, where buses[i] represents the departure time of the ith bus. You are also given a 0-indexed integer array passengers of length m, where passengers[j] represents the arrival time of the jth passenger. All bus departure times are unique. All passenger arrival times are unique.
You are given an integer capacity, which represents the maximum number of passengers that can get on each bus.
The passengers will get on the next available bus. You can get on a bus that will depart at x minutes if you arrive at y minutes where y <= x, and the bus is not full. Passengers with the earliest arrival times get on the bus first.
Return the latest time you may arrive at the bus station to catch a bus. You cannot arrive at the same time as another passenger.
Note: The arrays buses and passengers are not necessarily sorted.
Example 1:
Input: buses = [10,20], passengers = [2,17,18,19], capacity = 2
Output: 16
Explanation:
The 1st bus departs with the 1st passenger.
The 2nd bus departs with you and the 2nd passenger.
Note that you must not arrive at the same time as the passengers, which is why you must arrive before the 2nd passenger to catch the bus.Example 2:
Input: buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
Output: 20
Explanation:
The 1st bus departs with the 4th passenger.
The 2nd bus departs with the 6th and 2nd passengers.
The 3rd bus departs with the 1st passenger and you.
Constraints:
n == buses.lengthm == passengers.length1 <= n, m, capacity <= 1052 <= buses[i], passengers[i] <= 109- Each element in
busesis unique. - Each element in
passengersis unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int latestTimeCatchTheBus(vector<int> &buses, vector<int> &passengers, int capacity) {
sort(all(buses));
sort(all(passengers));
int n = int(buses.size());
int m = int(passengers.size());
auto vis = map<int, bool>();
int res = 1;
for (int i = 0, j = -1; i < n; ++i) {
int o = 0;
for (; o < capacity && j + 1 < m && passengers[j + 1] <= buses[i];) {
o++;
j++;
vis[passengers[j]] = 1;
if (vis[passengers[j] - 1] == 0) {
res = max(res, passengers[j] - 1);
}
}
if (o + 1 <= capacity && vis[buses[i]] == 0) {
res = max(res, buses[i]);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 最小差值平方和
- Difficulty: Medium
- Tag:
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度为 n 。
数组 nums1 和 nums2 的 差值平方和 定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])2 之和。
同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的,你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。
请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小 差值平方和 。
注意:你可以将数组中的元素变成 负 整数。
示例 1:
输入:nums1 = [1,2,3,4], nums2 = [2,10,20,19], k1 = 0, k2 = 0
输出:579
解释:nums1 和 nums2 中的元素不能修改,因为 k1 = 0 和 k2 = 0 。
差值平方和为:(1 - 2)2 + (2 - 10)2 + (3 - 20)2 + (4 - 19)2 = 579 。
示例 2:
输入:nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
输出:43
解释:一种得到最小差值平方和的方式为:
- 将 nums1[0] 增加一次。
- 将 nums2[2] 增加一次。
最小差值平方和为:
(2 - 5)2 + (4 - 8)2 + (10 - 7)2 + (12 - 9)2 = 43 。
注意,也有其他方式可以得到最小差值平方和,但没有得到比 43 更小答案的方案。
提示:
n == nums1.length == nums2.length1 <= n <= 1050 <= nums1[i], nums2[i] <= 1050 <= k1, k2 <= 109
Metadata
- Link: Minimum Sum of Squared Difference
- Difficulty: Medium
- Tag:
You are given two positive 0-indexed integer arrays nums1 and nums2, both of length n.
The sum of squared difference of arrays nums1 and nums2 is defined as the sum of (nums1[i] - nums2[i])2 for each 0 <= i < n.
You are also given two positive integers k1 and k2. You can modify any of the elements of nums1 by +1 or -1 at most k1 times. Similarly, you can modify any of the elements of nums2 by +1 or -1 at most k2 times.
Return the minimum sum of squared difference after modifying array nums1 at most k1 times and modifying array nums2 at most k2 times.
Note: You are allowed to modify the array elements to become negative integers.
Example 1:
Input: nums1 = [1,2,3,4], nums2 = [2,10,20,19], k1 = 0, k2 = 0
Output: 579
Explanation: The elements in nums1 and nums2 cannot be modified because k1 = 0 and k2 = 0.
The sum of square difference will be: (1 - 2)2 + (2 - 10)2 + (3 - 20)2 + (4 - 19)2 = 579.
Example 2:
Input: nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
Output: 43
Explanation: One way to obtain the minimum sum of square difference is:
- Increase nums1[0] once.
- Increase nums2[2] once.
The minimum of the sum of square difference will be:
(2 - 5)2 + (4 - 8)2 + (10 - 7)2 + (12 - 9)2 = 43.
Note that, there are other ways to obtain the minimum of the sum of square difference, but there is no way to obtain a sum smaller than 43.
Constraints:
n == nums1.length == nums2.length1 <= n <= 1050 <= nums1[i], nums2[i] <= 1050 <= k1, k2 <= 109
Solution
#include <bits/stdc++.h>
#include <cmath>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <functional>
#include <queue>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long minSumSquareDiff(vector<int> &nums1, vector<int> &nums2, int k1, int k2) {
int n = (int)(nums1.size());
vector<int> f;
f.reserve(n);
for (int i = 0; i < n; i++) {
f.push_back(abs(nums1[i] - nums2[i]));
}
f.push_back(0);
sort(all(f));
priority_queue<int, vector<int>, less<int>> pq;
ll k = k1 + k2;
int cnt = 1;
ll num = f[n];
for (int i = n - 1; i >= 0; i--) {
ll c = (num - f[i]) * cnt;
if (k >= c) {
k -= c;
++cnt;
num = f[i];
} else {
ll x = k / cnt;
num -= x;
k -= x * cnt;
for (int j = 0; j <= i; j++) {
pq.push(f[j]);
}
for (int j = 1; j <= cnt; j++) {
pq.push(int(num));
}
break;
}
}
if (cnt == n + 1) {
for (int j = 1; j <= cnt; j++) {
pq.push(int(num));
}
}
while (k && !pq.empty()) {
auto t = pq.top();
pq.pop();
if (t > 0) {
pq.push(t - 1);
k--;
}
}
ll res = 0;
while (!pq.empty()) {
int x = pq.top();
pq.pop();
res += 1ll * x * x;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 元素值大于变化阈值的子数组
- Difficulty: Hard
- Tag:
给你一个整数数组 nums 和一个整数 threshold 。
找到长度为 k 的 nums 子数组,满足数组中 每个 元素都 大于 threshold / k 。
请你返回满足要求的 任意 子数组的 大小 。如果没有这样的子数组,返回 -1 。
子数组 是数组中一段连续非空的元素序列。
示例 1:
输入:nums = [1,3,4,3,1], threshold = 6
输出:3
解释:子数组 [3,4,3] 大小为 3 ,每个元素都大于 6 / 3 = 2 。
注意这是唯一合法的子数组。
示例 2:
输入:nums = [6,5,6,5,8], threshold = 7
输出:1
解释:子数组 [8] 大小为 1 ,且 8 > 7 / 1 = 7 。所以返回 1 。
注意子数组 [6,5] 大小为 2 ,每个元素都大于 7 / 2 = 3.5 。
类似的,子数组 [6,5,6] ,[6,5,6,5] ,[6,5,6,5,8] 都是符合条件的子数组。
所以返回 2, 3, 4 和 5 都可以。
提示:
1 <= nums.length <= 1051 <= nums[i], threshold <= 109
Metadata
- Link: Subarray With Elements Greater Than Varying Threshold
- Difficulty: Hard
- Tag:
You are given an integer array nums and an integer threshold.
Find any subarray of nums of length k such that every element in the subarray is greater than threshold / k.
Return the size of any such subarray. If there is no such subarray, return -1.
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
Input: nums = [1,3,4,3,1], threshold = 6
Output: 3
Explanation: The subarray [3,4,3] has a size of 3, and every element is greater than 6 / 3 = 2.
Note that this is the only valid subarray.
Example 2:
Input: nums = [6,5,6,5,8], threshold = 7
Output: 1
Explanation: The subarray [8] has a size of 1, and 8 > 7 / 1 = 7. So 1 is returned.
Note that the subarray [6,5] has a size of 2, and every element is greater than 7 / 2 = 3.5.
Similarly, the subarrays [6,5,6], [6,5,6,5], [6,5,6,5,8] also satisfy the given conditions.
Therefore, 2, 3, 4, or 5 may also be returned.
Constraints:
1 <= nums.length <= 1051 <= nums[i], threshold <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int th, res;
struct Cartesian_Tree {
struct node {
int id, val, fa;
int son[2];
node() {}
node(int id, int val, int fa) : id(id), val(val), fa(fa) {
son[0] = son[1] = 0;
}
bool operator<(const node &other) const {
return val < other.val;
}
} t[N];
int root;
void init() {
t[0] = node(0, -INF, 0);
}
void build(vector<int> &a) {
int n = int(a.size());
for (int i = 1; i <= n; ++i) {
t[i] = node(i, a[i - 1], 0);
}
for (int i = 1; i <= n; ++i) {
int k = i - 1;
while (t[i] < t[k]) {
k = t[k].fa;
}
t[i].son[0] = t[k].son[1];
t[k].son[1] = i;
t[i].fa = k;
t[t[i].son[0]].fa = i;
}
root = t[0].son[1];
}
int DFS(int u) {
if (!u)
return 0;
int sze = DFS(t[u].son[0]) + DFS(t[u].son[1]) + 1;
if (t[u].val > th / sze) {
res = sze;
}
return sze;
}
} CT;
class Solution {
public:
int validSubarraySize(vector<int> &nums, int threshold) {
CT.init();
CT.build(nums);
res = -1;
th = threshold;
CT.DFS(CT.root);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif