weekly-contest-300

A

Statement

简体中文English

Metadata

Link: 解密消息
Difficulty: Easy
Tag:

给你字符串 key 和 message ，分别表示一个加密密钥和一段加密消息。解密 message 的步骤如下：

使用 key 中 26 个英文小写字母第一次出现的顺序作为替换表中的字母顺序。
将替换表与普通英文字母表对齐，形成对照表。
按照对照表替换 message 中的每个字母。
空格 ' ' 保持不变。

例如，key = "happy boy"（实际的加密密钥会包含字母表中每个字母 至少一次），据此，可以得到部分对照表（'h' -> 'a'、'a' -> 'b'、'p' -> 'c'、'y' -> 'd'、'b' -> 'e'、'o' -> 'f'）。

返回解密后的消息。

示例 1：

输入：key = "the quick brown fox jumps over the lazy dog", message = "vkbs bs t suepuv"
输出："this is a secret"
解释：对照表如上图所示。
提取 "the quick brown fox jumps over the lazy dog" 中每个字母的首次出现可以得到替换表。

示例 2：

输入：key = "eljuxhpwnyrdgtqkviszcfmabo", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb"
输出："the five boxing wizards jump quickly"
解释：对照表如上图所示。
提取 "eljuxhpwnyrdgtqkviszcfmabo" 中每个字母的首次出现可以得到替换表。

提示：

26 <= key.length <= 2000
key 由小写英文字母及 ' ' 组成
key 包含英文字母表中每个字符（'a' 到 'z'）至少一次
1 <= message.length <= 2000
message 由小写英文字母和 ' ' 组成

Metadata

Link: Decode the Message
Difficulty: Easy
Tag:

You are given the strings key and message, which represent a cipher key and a secret message, respectively. The steps to decode message are as follows:

Use the first appearance of all 26 lowercase English letters in key as the order of the substitution table.
Align the substitution table with the regular English alphabet.
Each letter in message is then substituted using the table.
Spaces ' ' are transformed to themselves.

For example, given key = "happy boy" (actual key would have at least one instance of each letter in the alphabet), we have the partial substitution table of ('h' -> 'a', 'a' -> 'b', 'p' -> 'c', 'y' -> 'd', 'b' -> 'e', 'o' -> 'f').

Return the decoded message.

Example 1:

Input: key = "the quick brown fox jumps over the lazy dog", message = "vkbs bs t suepuv"
Output: "this is a secret"
Explanation: The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "the quick brown fox jumps over the lazy dog".

Example 2:

Input: key = "eljuxhpwnyrdgtqkviszcfmabo", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb"
Output: "the five boxing wizards jump quickly"
Explanation: The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "eljuxhpwnyrdgtqkviszcfmabo".

Constraints:

26 <= key.length <= 2000
key consists of lowercase English letters and ' '.
key contains every letter in the English alphabet ('a' to 'z') at least once.
1 <= message.length <= 2000
message consists of lowercase English letters and ' '.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    string decodeMessage(string key, string message) {
        char ix = 'a';

        auto vis = vector<int>(255, 0);
        auto mp = vector<char>(255, 0);

        for (const char &c : key) {
            if (c == ' ') {
                continue;
            }

            if (ix > 'z') {
                break;
            }

            if (vis[c]) {
                continue;
            }

            vis[c] = 1;
            mp[c] = ix;
            ++ix;
        }

        for (auto &c : message) {
            if (c != ' ') {
                c = mp[c];
            }
        }

        return message;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 螺旋矩阵 IV
Difficulty: Medium
Tag:

给你两个整数：m 和 n ，表示矩阵的维数。

另给你一个整数链表的头节点 head 。

请你生成一个大小为 m x n 的螺旋矩阵，矩阵包含链表中的所有整数。链表中的整数从矩阵 左上角 开始、顺时针 按螺旋顺序填充。如果还存在剩余的空格，则用 -1 填充。

返回生成的矩阵。

示例 1：

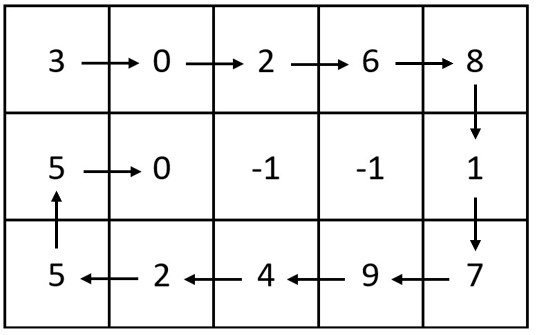
输入：m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
输出：[[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
解释：上图展示了链表中的整数在矩阵中是如何排布的。
注意，矩阵中剩下的空格用 -1 填充。

示例 2：

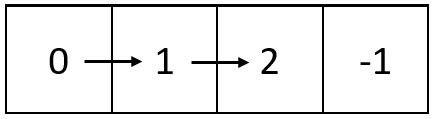
输入：m = 1, n = 4, head = [0,1,2]
输出：[[0,1,2,-1]]
解释：上图展示了链表中的整数在矩阵中是如何从左到右排布的。 
注意，矩阵中剩下的空格用 -1 填充。

提示：

1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
链表中节点数目在范围 [1, m * n] 内
0 <= Node.val <= 1000

Metadata

Link: Spiral Matrix IV
Difficulty: Medium
Tag:

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1:

Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2:

Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.

Constraints:

1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
The number of nodes in the list is in the range [1, m * n].
0 <= Node.val <= 1000

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

#ifdef LOCAL

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

#endif

int dir[][2] = {
        {0, 1},
        {1, 0},
        {0, -1},
        {-1, 0},
};

class Solution {
public:
    vector<vector<int>> spiralMatrix(int m, int n, ListNode *head) {
        auto res = vector<vector<int>>(m, vector<int>(n, -1));

        int x = 0, y = 0;
        int ix = 0;
        while (head) {
            res[x][y] = head->val;
            head = head->next;
            int nx, ny;
            nx = x + dir[ix][0];
            ny = y + dir[ix][1];

            if (nx < 0 || nx >= m || ny < 0 || ny >= n || res[nx][ny] != -1) {
                ix = (ix + 1) % 4;
                nx = x + dir[ix][0];
                ny = y + dir[ix][1];
            }

            x = nx;
            y = ny;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 知道秘密的人数
Difficulty: Medium
Tag:

在第 1 天，有一个人发现了一个秘密。

给你一个整数 delay ，表示每个人会在发现秘密后的 delay 天之后，每天给一个新的人分享秘密。同时给你一个整数 forget ，表示每个人在发现秘密 forget 天之后会忘记这个秘密。一个人不能在忘记秘密那一天及之后的日子里分享秘密。

给你一个整数 n ，请你返回在第 n 天结束时，知道秘密的人数。由于答案可能会很大，请你将结果对 10⁹ + 7 取余后返回。

示例 1：

输入：n = 6, delay = 2, forget = 4
输出：5
解释：
第 1 天：假设第一个人叫 A 。（一个人知道秘密）
第 2 天：A 是唯一一个知道秘密的人。（一个人知道秘密）
第 3 天：A 把秘密分享给 B 。（两个人知道秘密）
第 4 天：A 把秘密分享给一个新的人 C 。（三个人知道秘密）
第 5 天：A 忘记了秘密，B 把秘密分享给一个新的人 D 。（三个人知道秘密）
第 6 天：B 把秘密分享给 E，C 把秘密分享给 F 。（五个人知道秘密）

示例 2：

输入：n = 4, delay = 1, forget = 3
输出：6
解释：
第 1 天：第一个知道秘密的人为 A 。（一个人知道秘密）
第 2 天：A 把秘密分享给 B 。（两个人知道秘密）
第 3 天：A 和 B 把秘密分享给 2 个新的人 C 和 D 。（四个人知道秘密）
第 4 天：A 忘记了秘密，B、C、D 分别分享给 3 个新的人。（六个人知道秘密）

提示：

2 <= n <= 1000
1 <= delay < forget <= n

Metadata

Link: Number of People Aware of a Secret
Difficulty: Medium
Tag:

On day 1, one person discovers a secret.

You are given an integer delay, which means that each person will share the secret with a new person every day, starting from delay days after discovering the secret. You are also given an integer forget, which means that each person will forget the secret forget days after discovering it. A person cannot share the secret on the same day they forgot it, or on any day afterwards.

Given an integer n, return the number of people who know the secret at the end of day n. Since the answer may be very large, return it modulo 10⁹ + 7.

Example 1:

Input: n = 6, delay = 2, forget = 4
Output: 5
Explanation:
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)

Example 2:

Input: n = 4, delay = 1, forget = 3
Output: 6
Explanation:
Day 1: The first person is named A. (1 person)
Day 2: A shares the secret with B. (2 people)
Day 3: A and B share the secret with 2 new people, C and D. (4 people)
Day 4: A forgets the secret. B, C, and D share the secret with 3 new people. (6 people)

Constraints:

2 <= n <= 1000
1 <= delay < forget <= n

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

constexpr int mod = 1e9 + 7;

class Solution {
public:
    int peopleAwareOfSecret(int n, int delay, int forget) {
        auto f = vector<int>(n + 1, 0);
        auto g = vector<int>(n + 1, 0);
        auto h = vector<int>(n + 1, 0);

        g[1] = 1;

        for (int i = 1; i <= n; i++) {
            for (int j = i + delay; j <= min(n, i + forget - 1); j++) {
                g[j] += g[i];
                g[j] %= mod;
            }

            if (i + forget <= n) {
                h[i + forget] += g[i];
                h[i + forget] %= mod;
            }

            f[i] += (f[i - 1] + g[i]) % mod;
            f[i] %= mod;
            f[i] -= h[i];
            f[i] += mod;
            f[i] %= mod;
        }

        return f[n];
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 网格图中递增路径的数目
Difficulty: Hard
Tag:

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从任意格子出发，达到任意格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 10⁹ + 7 取余后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

示例 1：

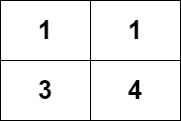
输入：grid = [[1,1],[3,4]]
输出：8
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[1]，[3]，[4] 。
- 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。
- 长度为 3 的路径：[1 -> 3 -> 4] 。
路径数目为 4 + 3 + 1 = 8 。

示例 2：

输入：grid = [[1],[2]]
输出：3
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[2] 。
- 长度为 2 的路径：[1 -> 2] 。
路径数目为 2 + 1 = 3 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 10⁵
1 <= grid[i][j] <= 10⁵

Metadata

Link: Number of Increasing Paths in a Grid
Difficulty: Hard
Tag:

You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.

Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 10⁹ + 7.

Two paths are considered different if they do not have exactly the same sequence of visited cells.

Example 1:

Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [1], [3], [4].
- Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
- Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [2].
- Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 10⁵
1 <= grid[i][j] <= 10⁵

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <queue>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

constexpr int mod = 1e9 + 7;

struct node {
    int x, y, v;
    node(int x, int y, int v) : x(x), y(y), v(v) {}
    bool operator<(const node &other) const {
        return v < other.v;
    }
};

int dir[][2] = {
        {0, 1},
        {0, -1},
        {1, 0},
        {-1, 0},
};

class Solution {
public:
    int countPaths(vector<vector<int>> &grid) {
        int m = int(grid.size());
        int n = int(grid[0].size());

        auto vec = vector<node>();
        vec.reserve(m * n);

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                vec.emplace_back(i, j, grid[i][j]);
            }
        }

        sort(all(vec));

        auto f = vector<vector<int>>(m + 1, vector<int>(n + 1, 1));
        int res = 0;

        for (auto &a : vec) {
            for (int i = 0; i < 4; i++) {
                int nx = a.x + dir[i][0];
                int ny = a.y + dir[i][1];

                if (nx < 0 || nx >= m || ny < 0 || ny >= n) {
                    continue;
                }

                if (a.v >= grid[nx][ny]) {
                    continue;
                }

                f[nx][ny] += f[a.x][a.y];
                f[nx][ny] %= mod;
            }

            res += f[a.x][a.y];
            res %= mod;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023