weekly-contest-275
A
Statement
Metadata
- Link: 检查是否每一行每一列都包含全部整数
- Difficulty: Easy
- Tag:
数组哈希表矩阵
对一个大小为 n x n 的矩阵而言,如果其每一行和每一列都包含从 1 到 n 的 全部 整数(含 1 和 n),则认为该矩阵是一个 有效 矩阵。
给你一个大小为 n x n 的整数矩阵 matrix ,请你判断矩阵是否为一个有效矩阵:如果是,返回 true ;否则,返回 false 。
示例 1:
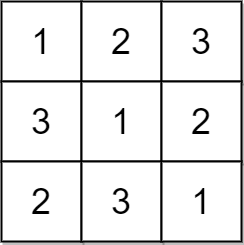
输入:matrix = [[1,2,3],[3,1,2],[2,3,1]]
输出:true
解释:在此例中,n = 3 ,每一行和每一列都包含数字 1、2、3 。
因此,返回 true 。
示例 2:
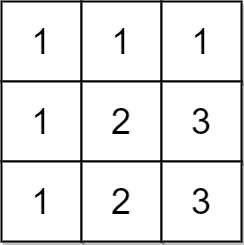
输入:matrix = [[1,1,1],[1,2,3],[1,2,3]]
输出:false
解释:在此例中,n = 3 ,但第一行和第一列不包含数字 2 和 3 。
因此,返回 false 。
提示:
n == matrix.length == matrix[i].length1 <= n <= 1001 <= matrix[i][j] <= n
Metadata
- Link: Check if Every Row and Column Contains All Numbers
- Difficulty: Easy
- Tag:
ArrayHash TableMatrix
An n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).
Given an n x n integer matrix matrix, return true if the matrix is valid. Otherwise, return false.
Example 1:

Input: matrix = [[1,2,3],[3,1,2],[2,3,1]]
Output: true
Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3.
Hence, we return true.
Example 2:

Input: matrix = [[1,1,1],[1,2,3],[1,2,3]]
Output: false
Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3.
Hence, we return false.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 1001 <= matrix[i][j] <= n
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
constexpr int N = 110;
vector<bool> has;
class Solution {
public:
bool checkValid(vector<vector<int>> &matrix) {
size_t n = matrix.size();
constexpr auto ok = [](const vector<bool> &has) {
size_t n = has.size();
for (int i = 1; i < n; ++i) {
if (!has[i]) {
return false;
}
}
return true;
};
for (int i = 0; i < n; i++) {
has = vector<bool>(n + 1, false);
for (int j = 0; j < n; j++) {
has[matrix[i][j]] = 1;
}
if (!ok(has)) {
return false;
}
}
for (int i = 0; i < n; i++) {
has = vector<bool>(n + 1, false);
for (int j = 0; j < n; j++) {
has[matrix[j][i]] = 1;
}
if (!ok(has)) {
return false;
}
}
return true;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 最少交换次数来组合所有的 1 II
- Difficulty: Medium
- Tag:
数组滑动窗口
交换 定义为选中一个数组中的两个 互不相同 的位置并交换二者的值。
环形 数组是一个数组,可以认为 第一个 元素和 最后一个 元素 相邻 。
给你一个 二进制环形 数组 nums ,返回在 任意位置 将数组中的所有 1 聚集在一起需要的最少交换次数。
示例 1:
输入:nums = [0,1,0,1,1,0,0]
输出:1
解释:这里列出一些能够将所有 1 聚集在一起的方案:
[0,0,1,1,1,0,0] 交换 1 次。
[0,1,1,1,0,0,0] 交换 1 次。
[1,1,0,0,0,0,1] 交换 2 次(利用数组的环形特性)。
无法在交换 0 次的情况下将数组中的所有 1 聚集在一起。
因此,需要的最少交换次数为 1 。
示例 2:
输入:nums = [0,1,1,1,0,0,1,1,0]
输出:2
解释:这里列出一些能够将所有 1 聚集在一起的方案:
[1,1,1,0,0,0,0,1,1] 交换 2 次(利用数组的环形特性)。
[1,1,1,1,1,0,0,0,0] 交换 2 次。
无法在交换 0 次或 1 次的情况下将数组中的所有 1 聚集在一起。
因此,需要的最少交换次数为 2 。
示例 3:
输入:nums = [1,1,0,0,1]
输出:0
解释:得益于数组的环形特性,所有的 1 已经聚集在一起。
因此,需要的最少交换次数为 0 。
提示:
1 <= nums.length <= 105nums[i]为0或者1
Metadata
- Link: Minimum Swaps to Group All 1's Together II
- Difficulty: Medium
- Tag:
ArraySliding Window
A swap is defined as taking two distinct positions in an array and swapping the values in them.
A circular array is defined as an array where we consider the first element and the last element to be adjacent.
Given a binary circular array nums, return the minimum number of swaps required to group all 1's present in the array together at any location.
Example 1:
Input: nums = [0,1,0,1,1,0,0]
Output: 1
Explanation: Here are a few of the ways to group all the 1's together:
[0,0,1,1,1,0,0] using 1 swap.
[0,1,1,1,0,0,0] using 1 swap.
[1,1,0,0,0,0,1] using 2 swaps (using the circular property of the array).
There is no way to group all 1's together with 0 swaps.
Thus, the minimum number of swaps required is 1.
Example 2:
Input: nums = [0,1,1,1,0,0,1,1,0]
Output: 2
Explanation: Here are a few of the ways to group all the 1's together:
[1,1,1,0,0,0,0,1,1] using 2 swaps (using the circular property of the array).
[1,1,1,1,1,0,0,0,0] using 2 swaps.
There is no way to group all 1's together with 0 or 1 swaps.
Thus, the minimum number of swaps required is 2.
Example 3:
Input: nums = [1,1,0,0,1]
Output: 0
Explanation: All the 1's are already grouped together due to the circular property of the array.
Thus, the minimum number of swaps required is 0.
Constraints:
1 <= nums.length <= 105nums[i]is either0or1.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minSwaps(vector<int> &nums) {
int n = nums.size();
int m = 0;
for (auto &a : nums) m += a;
vector<int> sum(n * 2 + 1, 0);
for (int i = 1; i <= n * 2; i++) {
sum[i] = sum[i - 1] + (nums[(i - 1) % n] == 0);
}
int res = n;
for (int i = 0; i < n; i++) {
res = min(res, sum[i + m] - sum[i]);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 统计追加字母可以获得的单词数
- Difficulty: Medium
- Tag:
位运算数组哈希表字符串排序
给你两个下标从 0 开始的字符串数组 startWords 和 targetWords 。每个字符串都仅由 小写英文字母 组成。
对于 targetWords 中的每个字符串,检查是否能够从 startWords 中选出一个字符串,执行一次 转换操作 ,得到的结果与当前 targetWords 字符串相等。
转换操作 如下面两步所述:
- 追加 任何 不存在 于当前字符串的任一小写字母到当前字符串的末尾。
- 例如,如果字符串为
"abc",那么字母'd'、'e'或'y'都可以加到该字符串末尾,但'a'就不行。如果追加的是'd',那么结果字符串为"abcd"。
- 例如,如果字符串为
- 重排 新字符串中的字母,可以按 任意 顺序重新排布字母。
- 例如,
"abcd"可以重排为"acbd"、"bacd"、"cbda",以此类推。注意,它也可以重排为"abcd"自身。
- 例如,
找出 targetWords 中有多少字符串能够由 startWords 中的 任一 字符串执行上述转换操作获得。返回 targetWords 中这类 字符串的数目 。
注意:你仅能验证 targetWords 中的字符串是否可以由 startWords 中的某个字符串经执行操作获得。startWords 中的字符串在这一过程中 不 发生实际变更。
示例 1:
输入:startWords = ["ant","act","tack"], targetWords = ["tack","act","acti"]
输出:2
解释:
- 为了形成 targetWords[0] = "tack" ,可以选用 startWords[1] = "act" ,追加字母 'k' ,并重排 "actk" 为 "tack" 。
- startWords 中不存在可以用于获得 targetWords[1] = "act" 的字符串。
注意 "act" 确实存在于 startWords ,但是 必须 在重排前给这个字符串追加一个字母。
- 为了形成 targetWords[2] = "acti" ,可以选用 startWords[1] = "act" ,追加字母 'i' ,并重排 "acti" 为 "acti" 自身。
示例 2:
输入:startWords = ["ab","a"], targetWords = ["abc","abcd"]
输出:1
解释:
- 为了形成 targetWords[0] = "abc" ,可以选用 startWords[0] = "ab" ,追加字母 'c' ,并重排为 "abc" 。
- startWords 中不存在可以用于获得 targetWords[1] = "abcd" 的字符串。
提示:
1 <= startWords.length, targetWords.length <= 5 * 1041 <= startWords[i].length, targetWords[j].length <= 26startWords和targetWords中的每个字符串都仅由小写英文字母组成- 在
startWords或targetWords的任一字符串中,每个字母至多出现一次
Metadata
- Link: Count Words Obtained After Adding a Letter
- Difficulty: Medium
- Tag:
Bit ManipulationArrayHash TableStringSorting
You are given two 0-indexed arrays of strings startWords and targetWords. Each string consists of lowercase English letters only.
For each string in targetWords, check if it is possible to choose a string from startWords and perform a conversion operation on it to be equal to that from targetWords.
The conversion operation is described in the following two steps:
- Append any lowercase letter that is not present in the string to its end.
- For example, if the string is
"abc", the letters'd','e', or'y'can be added to it, but not'a'. If'd'is added, the resulting string will be"abcd".
- For example, if the string is
- Rearrange the letters of the new string in any arbitrary order.
- For example,
"abcd"can be rearranged to"acbd","bacd","cbda", and so on. Note that it can also be rearranged to"abcd"itself.
- For example,
Return the number of strings in targetWords that can be obtained by performing the operations on any string of startWords.
Note that you will only be verifying if the string in targetWords can be obtained from a string in startWords by performing the operations. The strings in startWords do not actually change during this process.
Example 1:
Input: startWords = ["ant","act","tack"], targetWords = ["tack","act","acti"]
Output: 2
Explanation:
- In order to form targetWords[0] = "tack", we use startWords[1] = "act", append 'k' to it, and rearrange "actk" to "tack".
- There is no string in startWords that can be used to obtain targetWords[1] = "act".
Note that "act" does exist in startWords, but we must append one letter to the string before rearranging it.
- In order to form targetWords[2] = "acti", we use startWords[1] = "act", append 'i' to it, and rearrange "acti" to "acti" itself.
Example 2:
Input: startWords = ["ab","a"], targetWords = ["abc","abcd"]
Output: 1
Explanation:
- In order to form targetWords[0] = "abc", we use startWords[0] = "ab", add 'c' to it, and rearrange it to "abc".
- There is no string in startWords that can be used to obtain targetWords[1] = "abcd".
Constraints:
1 <= startWords.length, targetWords.length <= 5 * 1041 <= startWords[i].length, targetWords[j].length <= 26- Each string of
startWordsandtargetWordsconsists of lowercase English letters only. - No letter occurs more than once in any string of
startWordsortargetWords.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int wordCount(vector<string>& startWords, vector<string>& targetWords) {
unordered_map<int, bool> hs;
for (auto& s : startWords) {
int mask = 0;
for (auto& c : s) mask |= (1 << (c - 'a'));
hs[mask] = 1;
}
int res = 0;
for (auto& s : targetWords) {
int mask = 0;
for (auto& c : s) mask |= (1 << (c - 'a'));
for (int i = 0; i < 26; i++) {
if (((mask >> i) & 1) == 1)
if (hs.count(mask ^ (1 << i))) {
res++;
break;
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 全部开花的最早一天
- Difficulty: Hard
- Tag:
贪心数组排序
你有 n 枚花的种子。每枚种子必须先种下,才能开始生长、开花。播种需要时间,种子的生长也是如此。给你两个下标从 0 开始的整数数组 plantTime 和 growTime ,每个数组的长度都是 n :
plantTime[i]是 播种 第i枚种子所需的 完整天数 。每天,你只能为播种某一枚种子而劳作。无须 连续几天都在种同一枚种子,但是种子播种必须在你工作的天数达到plantTime[i]之后才算完成。growTime[i]是第i枚种子完全种下后生长所需的 完整天数 。在它生长的最后一天 之后 ,将会开花并且永远 绽放 。
从第 0 开始,你可以按 任意 顺序播种种子。
返回所有种子都开花的 最早 一天是第几天。
示例 1:
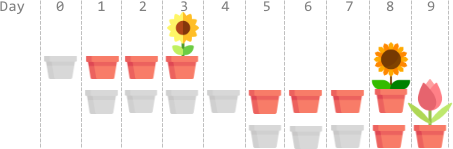
输入:plantTime = [1,4,3], growTime = [2,3,1]
输出:9
解释:灰色的花盆表示播种的日子,彩色的花盆表示生长的日子,花朵表示开花的日子。
一种最优方案是:
第 0 天,播种第 0 枚种子,种子生长 2 整天。并在第 3 天开花。
第 1、2、3、4 天,播种第 1 枚种子。种子生长 3 整天,并在第 8 天开花。
第 5、6、7 天,播种第 2 枚种子。种子生长 1 整天,并在第 9 天开花。
因此,在第 9 天,所有种子都开花。
示例 2:
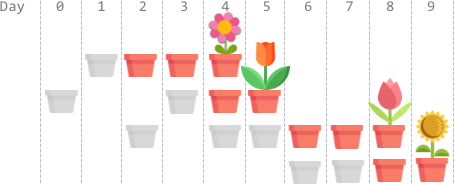
输入:plantTime = [1,2,3,2], growTime = [2,1,2,1]
输出:9
解释:灰色的花盆表示播种的日子,彩色的花盆表示生长的日子,花朵表示开花的日子。
一种最优方案是:
第 1 天,播种第 0 枚种子,种子生长 2 整天。并在第 4 天开花。
第 0、3 天,播种第 1 枚种子。种子生长 1 整天,并在第 5 天开花。
第 2、4、5 天,播种第 2 枚种子。种子生长 2 整天,并在第 8 天开花。
第 6、7 天,播种第 3 枚种子。种子生长 1 整天,并在第 9 天开花。
因此,在第 9 天,所有种子都开花。
示例 3:
输入:plantTime = [1], growTime = [1]
输出:2
解释:第 0 天,播种第 0 枚种子。种子需要生长 1 整天,然后在第 2 天开花。
因此,在第 2 天,所有种子都开花。
提示:
n == plantTime.length == growTime.length1 <= n <= 1051 <= plantTime[i], growTime[i] <= 104
Metadata
- Link: Earliest Possible Day of Full Bloom
- Difficulty: Hard
- Tag:
GreedyArraySorting
You have n flower seeds. Every seed must be planted first before it can begin to grow, then bloom. Planting a seed takes time and so does the growth of a seed. You are given two 0-indexed integer arrays plantTime and growTime, of length n each:
plantTime[i]is the number of full days it takes you to plant theithseed. Every day, you can work on planting exactly one seed. You do not have to work on planting the same seed on consecutive days, but the planting of a seed is not complete until you have workedplantTime[i]days on planting it in total.growTime[i]is the number of full days it takes theithseed to grow after being completely planted. After the last day of its growth, the flower blooms and stays bloomed forever.
From the beginning of day 0, you can plant the seeds in any order.
Return the earliest possible day where all seeds are blooming.
Example 1:

Input: plantTime = [1,4,3], growTime = [2,3,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 0, plant the 0th seed. The seed grows for 2 full days and blooms on day 3.
On days 1, 2, 3, and 4, plant the 1st seed. The seed grows for 3 full days and blooms on day 8.
On days 5, 6, and 7, plant the 2nd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.
Example 2:

Input: plantTime = [1,2,3,2], growTime = [2,1,2,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 1, plant the 0th seed. The seed grows for 2 full days and blooms on day 4.
On days 0 and 3, plant the 1st seed. The seed grows for 1 full day and blooms on day 5.
On days 2, 4, and 5, plant the 2nd seed. The seed grows for 2 full days and blooms on day 8.
On days 6 and 7, plant the 3rd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.
Example 3:
Input: plantTime = [1], growTime = [1]
Output: 2
Explanation: On day 0, plant the 0th seed. The seed grows for 1 full day and blooms on day 2.
Thus, on day 2, all the seeds are blooming.
Constraints:
n == plantTime.length == growTime.length1 <= n <= 1051 <= plantTime[i], growTime[i] <= 104
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct node {
int a;
int b;
};
class Solution {
public:
int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
int n = plantTime.size();
vector<node> node_list;
for (int i = 0; i < n; i++) {
node_list.emplace_back(node{.a = plantTime[i], .b = growTime[i]});
}
sort(All(node_list), [&](const node& a, const node& b) {
return a.b > b.b;
});
int res = 0;
int sum = 0;
for (auto& a : node_list) {
res = max(res, sum + a.a + a.b);
sum += a.a;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif