biweekly-contest-92

A

Statement

简体中文English

Metadata

• Link: 分割圆的最少切割次数
• Difficulty: Easy
• Tag:

圆内一个 有效切割 ，符合以下二者之一：

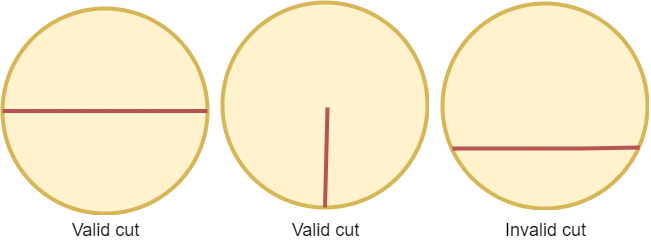
• 该切割是两个端点在圆上的线段，且该线段经过圆心。
• 该切割是一端在圆心另一端在圆上的线段。

一些有效和无效的切割如下图所示。

给你一个整数 n ，请你返回将圆切割成相等的 n 等分的 最少 切割次数。

 

示例 1：

输入：n = 4
输出：2
解释：
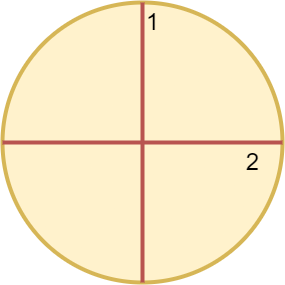
上图展示了切割圆 2 次，得到四等分。

示例 2：

输入：n = 3
输出：3
解释：
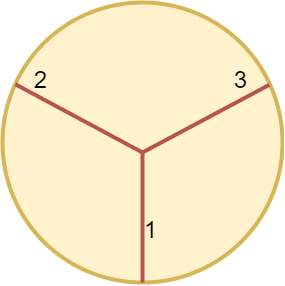
最少需要切割 3 次，将圆切成三等分。
少于 3 次切割无法将圆切成大小相等面积相同的 3 等分。
同时可以观察到，第一次切割无法将圆切割开。

 

提示：

• 1 <= n <= 100

Metadata

• Link: Minimum Cuts to Divide a Circle
• Difficulty: Easy
• Tag:

A valid cut in a circle can be:

• A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or
• A cut that is represented by a straight line that touches one point on the edge of the circle and its center.

Some valid and invalid cuts are shown in the figures below.

Given the integer n, return the minimum number of cuts needed to divide a circle into n equal slices.

 

Example 1:

Input: n = 4
Output: 2
Explanation: 
The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices.

Example 2:

Input: n = 3
Output: 3
Explanation:
At least 3 cuts are needed to divide the circle into 3 equal slices. 
It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape.
Also note that the first cut will not divide the circle into distinct parts.

 

Constraints:

• 1 <= n <= 100

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int numberOfCuts(int n) {
        if (n < 3) {
            return n - 1;
        }

        if (n & 1) {
            return n;
        }

        return n >> 1;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

• Link: 行和列中一和零的差值
• Difficulty: Medium
• Tag:

给你一个下标从 0 开始的 m x n 二进制矩阵 grid 。

我们按照如下过程，定义一个下标从 0 开始的 m x n 差值矩阵 diff ：

• 令第 i 行一的数目为 onesRowi 。
• 令第 j 列一的数目为 onesColj 。
• 令第 i 行零的数目为 zerosRowi 。
• 令第 j 列零的数目为 zerosColj 。
• diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj

请你返回差值矩阵 diff 。

 

示例 1：

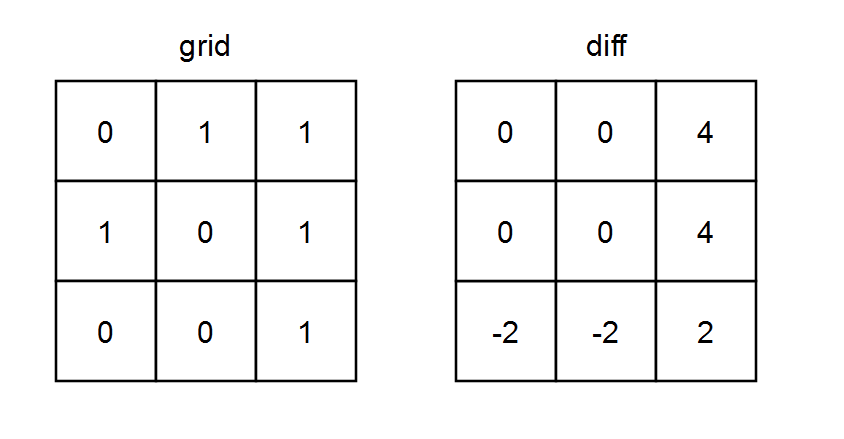
输入：grid = [[0,1,1],[1,0,1],[0,0,1]]
输出：[[0,0,4],[0,0,4],[-2,-2,2]]
解释：
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2

示例 2：

输入：grid = [[1,1,1],[1,1,1]]
输出：[[5,5,5],[5,5,5]]
解释：
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• grid[i][j] 要么是 0 ，要么是 1 。

Metadata

• Link: Difference Between Ones and Zeros in Row and Column
• Difficulty: Medium
• Tag:

You are given a 0-indexed m x n binary matrix grid.

A 0-indexed m x n difference matrix diff is created with the following procedure:

• Let the number of ones in the ith row be onesRowi.
• Let the number of ones in the jth column be onesColj.
• Let the number of zeros in the ith row be zerosRowi.
• Let the number of zeros in the jth column be zerosColj.
• diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj

Return the difference matrix diff.

 

Example 1:

Input: grid = [[0,1,1],[1,0,1],[0,0,1]]
Output: [[0,0,4],[0,0,4],[-2,-2,2]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2

Example 2:

Input: grid = [[1,1,1],[1,1,1]]
Output: [[5,5,5],[5,5,5]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• grid[i][j] is either 0 or 1.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    vector<vector<int>> onesMinusZeros(vector<vector<int>> &grid) {
        int n = int(grid.size());
        int m = int(grid[0].size());

        auto res = vector<vector<int>>(n, vector<int>(m, 0));
        auto row = vector<vector<int>>(n, vector<int>(2, 0));
        auto col = vector<vector<int>>(m, vector<int>(2, 0));

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int x = grid[i][j];
                ++row[i][x];
                ++col[j][x];
            }
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                res[i][j] = row[i][1] + col[j][1] - row[i][0] - col[j][0];
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

• Link: 商店的最少代价
• Difficulty: Medium
• Tag:

给你一个顾客访问商店的日志，用一个下标从 0 开始且只包含字符 'N' 和 'Y' 的字符串 customers 表示：

• 如果第 i 个字符是 'Y' ，它表示第 i 小时有顾客到达。
• 如果第 i 个字符是 'N' ，它表示第 i 小时没有顾客到达。

如果商店在第 j 小时关门（0 <= j <= n），代价按如下方式计算：

• 在开门期间，如果某一个小时没有顾客到达，代价增加 1 。
• 在关门期间，如果某一个小时有顾客到达，代价增加 1 。

请你返回在确保代价 最小 的前提下，商店的 最早 关门时间。

注意，商店在第 j 小时关门表示在第 j 小时以及之后商店处于关门状态。

 

示例 1：

输入：customers = "YYNY"
输出：2
解释：
- 第 0 小时关门，总共 1+1+0+1 = 3 代价。
- 第 1 小时关门，总共 0+1+0+1 = 2 代价。
- 第 2 小时关门，总共 0+0+0+1 = 1 代价。
- 第 3 小时关门，总共 0+0+1+1 = 2 代价。
- 第 4 小时关门，总共 0+0+1+0 = 1 代价。
在第 2 或第 4 小时关门代价都最小。由于第 2 小时更早，所以最优关门时间是 2 。

示例 2：

输入：customers = "NNNNN"
输出：0
解释：最优关门时间是 0 ，因为自始至终没有顾客到达。

示例 3：

输入：customers = "YYYY"
输出：4
解释：最优关门时间是 4 ，因为每一小时均有顾客到达。

 

提示：

• 1 <= customers.length <= 105
• customers 只包含字符 'Y' 和 'N' 。

Metadata

• Link: Minimum Penalty for a Shop
• Difficulty: Medium
• Tag:

You are given the customer visit log of a shop represented by a 0-indexed string customers consisting only of characters 'N' and 'Y':

• if the ith character is 'Y', it means that customers come at the ith hour
• whereas 'N' indicates that no customers come at the ith hour.

If the shop closes at the jth hour (0 <= j <= n), the penalty is calculated as follows:

• For every hour when the shop is open and no customers come, the penalty increases by 1.
• For every hour when the shop is closed and customers come, the penalty increases by 1.

Return the earliest hour at which the shop must be closed to incur a minimum penalty.

Note that if a shop closes at the jth hour, it means the shop is closed at the hour j.

 

Example 1:

Input: customers = "YYNY"
Output: 2
Explanation: 
- Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty.
- Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty.
- Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty.
- Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty.
- Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty.
Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2.

Example 2:

Input: customers = "NNNNN"
Output: 0
Explanation: It is best to close the shop at the 0th hour as no customers arrive.

Example 3:

Input: customers = "YYYY"
Output: 4
Explanation: It is best to close the shop at the 4th hour as customers arrive at each hour.

 

Constraints:

• 1 <= customers.length <= 105
• customers consists only of characters 'Y' and 'N'.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int bestClosingTime(string customers) {
        int n = int(customers.size());
        auto f = vector<int>(n + 5, 0);
        auto g = vector<int>(n + 5, 0);

        for (int i = 1; i <= n; i++) {
            f[i] = f[i - 1] + (customers[i - 1] == 'N');
        }

        for (int i = n; i >= 1; i--) {
            g[i] = g[i + 1] + (customers[i - 1] == 'Y');
        }

        int res = 0;
        int mx = g[1];

        for (int i = 1; i <= n; i++) {
            int cur = f[i] + g[i + 1];
            if (cur < mx) {
                mx = cur;
                res = i;
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

• Link: 统计回文子序列数目
• Difficulty: Hard
• Tag:

给你数字字符串 s ，请你返回 s 中长度为 5 的 回文子序列 数目。由于答案可能很大，请你将答案对 109 + 7 取余 后返回。

提示：

• 如果一个字符串从前往后和从后往前读相同，那么它是 回文字符串 。
• 子序列是一个字符串中删除若干个字符后，不改变字符顺序，剩余字符构成的字符串。

 

示例 1：

输入：s = "103301"
输出：2
解释：
总共有 6 长度为 5 的子序列："10330" ，"10331" ，"10301" ，"10301" ，"13301" ，"03301" 。
它们中有两个（都是 "10301"）是回文的。

示例 2：

输入：s = "0000000"
输出：21
解释：所有 21 个长度为 5 的子序列都是 "00000" ，都是回文的。

示例 3：

输入：s = "9999900000"
输出：2
解释：仅有的两个回文子序列是 "99999" 和 "00000" 。

 

提示：

• 1 <= s.length <= 104
• s 只包含数字字符。

Metadata

• Link: Count Palindromic Subsequences
• Difficulty: Hard
• Tag:

Given a string of digits s, return the number of palindromic subsequences of s having length 5. Since the answer may be very large, return it modulo 109 + 7.

Note:

• A string is palindromic if it reads the same forward and backward.
• A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.

 

Example 1:

Input: s = "103301"
Output: 2
Explanation: 
There are 6 possible subsequences of length 5: "10330","10331","10301","10301","13301","03301". 
Two of them (both equal to "10301") are palindromic.

Example 2:

Input: s = "0000000"
Output: 21
Explanation: All 21 subsequences are "00000", which is palindromic.

Example 3:

Input: s = "9999900000"
Output: 2
Explanation: The only two palindromic subsequences are "99999" and "00000".

 

Constraints:

• 1 <= s.length <= 104
• s consists of digits.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    static inline constexpr int mod = 1e9 + 7;
    int countPalindromes(string s) {
        int n = int(s.size());

        auto f = vector<vector<vector<int>>>(n + 5, vector<vector<int>>(10, vector<int>(10, 0)));
        auto g = vector<vector<vector<int>>>(n + 5, vector<vector<int>>(10, vector<int>(10, 0)));
        auto cnt = vector<int>(20, 0);

        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < 10; j++) {
                for (int k = 0; k < 10; k++) {
                    f[i][j][k] = f[i - 1][j][k];
                }
            }

            int num = s[i - 1] - '0';
            for (int j = 0; j < 10; j++) {
                (f[i][j][num] += cnt[j]) %= mod;
            }

            ++cnt[num];
        }

        cnt = vector<int>(20, 0);

        for (int i = n; i >= 1; i--) {
            for (int j = 0; j < 10; j++) {
                for (int k = 0; k < 10; k++) {
                    g[i][j][k] = g[i + 1][j][k];
                }
            }

            int num = s[i - 1] - '0';
            for (int j = 0; j < 10; j++) {
                (g[i][num][j] += cnt[j]) %= mod;
            }

            ++cnt[num];
        }

        ll res = 0;
        for (int i = 3; i <= n; i++) {
            for (int j = 0; j < 10; j++) {
                for (int k = 0; k < 10; k++) {
                    res += (1ll * f[i - 1][j][k] * g[i + 1][k][j]) % mod;
                    res %= mod;
                }
            }
        }

        return int(res);
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

---

最后更新: October 11, 2023