weekly-contest-202
A
Statement
Metadata
- Link: 存在连续三个奇数的数组
- Difficulty: Easy
- Tag:
数组
给你一个整数数组 arr,请你判断数组中是否存在连续三个元素都是奇数的情况:如果存在,请返回 true ;否则,返回 false 。
示例 1:
输入:arr = [2,6,4,1]
输出:false
解释:不存在连续三个元素都是奇数的情况。
示例 2:
输入:arr = [1,2,34,3,4,5,7,23,12]
输出:true
解释:存在连续三个元素都是奇数的情况,即 [5,7,23] 。
提示:
1 <= arr.length <= 10001 <= arr[i] <= 1000
Metadata
- Link: Three Consecutive Odds
- Difficulty: Easy
- Tag:
Array
Given an integer array arr, return true if there are three consecutive odd numbers in the array. Otherwise, return false.
Example 1:
Input: arr = [2,6,4,1]
Output: false
Explanation: There are no three consecutive odds.
Example 2:
Input: arr = [1,2,34,3,4,5,7,23,12]
Output: true
Explanation: [5,7,23] are three consecutive odds.
Constraints:
1 <= arr.length <= 10001 <= arr[i] <= 1000
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
class Solution {
public:
bool threeConsecutiveOdds(vector<int> &arr) {
int n = SZ(arr);
for (int i = 2; i < n; ++i) {
if (arr[i - 2] % 2 && arr[i - 1] % 2 && arr[i] % 2)
return true;
}
return false;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 使数组中所有元素相等的最小操作数
- Difficulty: Medium
- Tag:
数学
存在一个长度为 n 的数组 arr ,其中 arr[i] = (2 * i) + 1 ( 0 <= i < n )。
一次操作中,你可以选出两个下标,记作 x 和 y ( 0 <= x, y < n )并使 arr[x] 减去 1 、arr[y] 加上 1 (即 arr[x] -=1 且 arr[y] += 1 )。最终的目标是使数组中的所有元素都 相等 。题目测试用例将会 保证 :在执行若干步操作后,数组中的所有元素最终可以全部相等。
给你一个整数 n,即数组的长度。请你返回使数组 arr 中所有元素相等所需的 最小操作数 。
示例 1:
输入:n = 3
输出:2
解释:arr = [1, 3, 5]
第一次操作选出 x = 2 和 y = 0,使数组变为 [2, 3, 4]
第二次操作继续选出 x = 2 和 y = 0,数组将会变成 [3, 3, 3]
示例 2:
输入:n = 6
输出:9
提示:
1 <= n <= 10^4
Metadata
- Link: Minimum Operations to Make Array Equal
- Difficulty: Medium
- Tag:
Math
You have an array arr of length n where arr[i] = (2 * i) + 1 for all valid values of i (i.e., 0 <= i < n).
In one operation, you can select two indices x and y where 0 <= x, y < n and subtract 1 from arr[x] and add 1 to arr[y] (i.e., perform arr[x] -=1 and arr[y] += 1). The goal is to make all the elements of the array equal. It is guaranteed that all the elements of the array can be made equal using some operations.
Given an integer n, the length of the array, return the minimum number of operations needed to make all the elements of arr equal.
Example 1:
Input: n = 3
Output: 2
Explanation: arr = [1, 3, 5]
First operation choose x = 2 and y = 0, this leads arr to be [2, 3, 4]
In the second operation choose x = 2 and y = 0 again, thus arr = [3, 3, 3].
Example 2:
Input: n = 6
Output: 9
Constraints:
1 <= n <= 104
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;
int a[N];
class Solution {
public:
int minOperations(int n) {
if (n == 1)
return 0;
for (int i = 0; i < n; ++i) {
a[i] = 2 * i + 1;
}
int res = 0;
int mid = 0;
if (n & 1)
mid = a[n / 2];
else
mid = (a[n / 2] + a[n / 2 - 1]) / 2;
for (int i = 0; i < n; ++i) res += abs(a[i] - mid);
return res / 2;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 两球之间的磁力
- Difficulty: Medium
- Tag:
数组二分查找排序
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
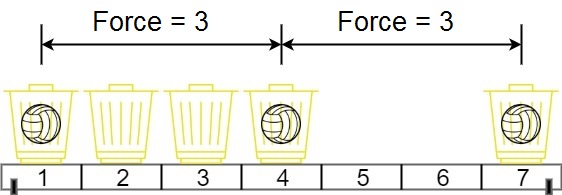
输入:position = [1,2,3,4,7], m = 3
输出:3
解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2
输出:999999999
解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
Metadata
- Link: Magnetic Force Between Two Balls
- Difficulty: Medium
- Tag:
ArrayBinary SearchSorting
In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.
Rick stated that magnetic force between two different balls at positions x and y is |x - y|.
Given the integer array position and the integer m. Return the required force.
Example 1:
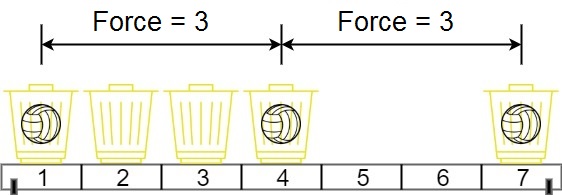
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
Example 2:
Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.
Constraints:
n == position.length2 <= n <= 1051 <= position[i] <= 109- All integers in
positionare distinct. 2 <= m <= position.length
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n, m, a[N];
bool ok(int x) {
if (m == 1)
return true;
int remind = m - 1;
int pre = a[1];
for (int i = 2; i <= n; ++i) {
if (a[i] - pre >= x) {
pre = a[i];
--remind;
if (!remind)
return true;
}
}
return false;
}
class Solution {
public:
int maxDistance(vector<int> &position, int _m) {
m = _m;
sort(all(position));
n = SZ(position);
for (int i = 1; i <= n; ++i) a[i] = position[i - 1];
int l = 0, r = 1e9, res = 0;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (ok(mid)) {
l = mid + 1;
res = mid;
} else {
r = mid - 1;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 吃掉 N 个橘子的最少天数
- Difficulty: Hard
- Tag:
记忆化搜索动态规划
厨房里总共有 n 个橘子,你决定每一天选择如下方式之一吃这些橘子:
- 吃掉一个橘子。
- 如果剩余橘子数
n能被 2 整除,那么你可以吃掉n/2个橘子。 - 如果剩余橘子数
n能被 3 整除,那么你可以吃掉2*(n/3)个橘子。
每天你只能从以上 3 种方案中选择一种方案。
请你返回吃掉所有 n 个橘子的最少天数。
示例 1:
输入:n = 10
输出:4
解释:你总共有 10 个橘子。
第 1 天:吃 1 个橘子,剩余橘子数 10 - 1 = 9。
第 2 天:吃 6 个橘子,剩余橘子数 9 - 2*(9/3) = 9 - 6 = 3。(9 可以被 3 整除)
第 3 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。
第 4 天:吃掉最后 1 个橘子,剩余橘子数 1 - 1 = 0。
你需要至少 4 天吃掉 10 个橘子。
示例 2:
输入:n = 6
输出:3
解释:你总共有 6 个橘子。
第 1 天:吃 3 个橘子,剩余橘子数 6 - 6/2 = 6 - 3 = 3。(6 可以被 2 整除)
第 2 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。(3 可以被 3 整除)
第 3 天:吃掉剩余 1 个橘子,剩余橘子数 1 - 1 = 0。
你至少需要 3 天吃掉 6 个橘子。
示例 3:
输入:n = 1
输出:1
示例 4:
输入:n = 56
输出:6
提示:
1 <= n <= 2*10^9
Metadata
- Link: Minimum Number of Days to Eat N Oranges
- Difficulty: Hard
- Tag:
MemoizationDynamic Programming
There are n oranges in the kitchen and you decided to eat some of these oranges every day as follows:
- Eat one orange.
- If the number of remaining oranges
nis divisible by2then you can eatn / 2oranges. - If the number of remaining oranges
nis divisible by3then you can eat2 * (n / 3)oranges.
You can only choose one of the actions per day.
Given the integer n, return the minimum number of days to eat n oranges.
Example 1:
Input: n = 10
Output: 4
Explanation: You have 10 oranges.
Day 1: Eat 1 orange, 10 - 1 = 9.
Day 2: Eat 6 oranges, 9 - 2*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1.
Day 4: Eat the last orange 1 - 1 = 0.
You need at least 4 days to eat the 10 oranges.
Example 2:
Input: n = 6
Output: 3
Explanation: You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange 1 - 1 = 0.
You need at least 3 days to eat the 6 oranges.
Constraints:
1 <= n <= 2 * 109
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;
map<int, int> f;
int dfs(int x) {
if (x == 0)
return 0;
if (x == 1)
return 1;
if (f.count(x))
return f[x];
int now = x;
if (x % 2 == 0)
chmin(now, dfs(x / 2) + 1);
if (x % 3 == 0)
chmin(now, dfs(x / 3) + 1);
if (x % 2 == 1)
chmin(now, dfs((x - 1) / 2) + 2);
if (x % 3 == 1)
chmin(now, dfs((x - 1) / 3) + 2);
if (x % 3 == 2)
chmin(now, dfs((x - 2) / 3) + 3);
return f[x] = now;
}
class Solution {
public:
int minDays(int n) {
f.clear();
return dfs(n);
// int res = n;
// int it = 1, now = 1;
// while (it < n) {
//
// }
// return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif