跳转至

110.balanced-binary-tree

Statement

Metadata
  • Link: 平衡二叉树
  • Difficulty: Easy
  • Tag: 树 深度优先搜索 二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

 

示例 1：

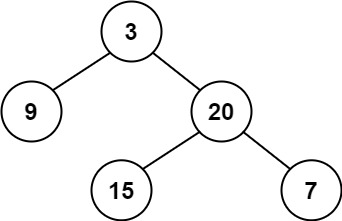
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

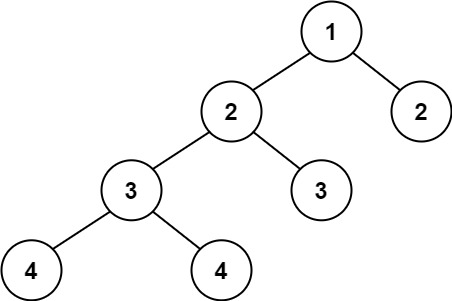
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

 

提示：

  • 树中的节点数在范围 [0, 5000] 内
  • -104 <= Node.val <= 104

Metadata

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

 

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

 

Constraints:

  • The number of nodes in the tree is in the range [0, 5000].
  • -104 <= Node.val <= 104

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

#ifdef LOCAL

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

#endif

class Solution {
public:
    bool isBalanced(TreeNode *root) {
        bool res = true;
        auto dfs = [&](auto self, TreeNode *rt) -> int {
            if (!rt) {
                return 0;
            }

            int l = self(self, rt->left);
            int r = self(self, rt->right);

            if (abs(l - r) > 1) {
                res = false;
            }

            return max(l, r) + 1;
        };

        dfs(dfs, root);
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部