119.pascals-triangle-ii
Statement
Metadata
- Link: 杨辉三角 II
- Difficulty: Easy
- Tag:
数组动态规划
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
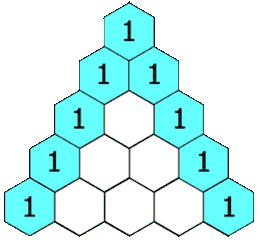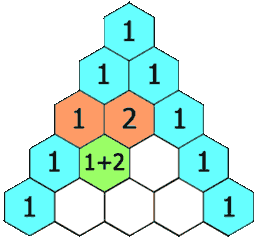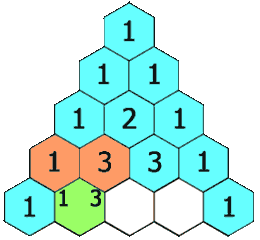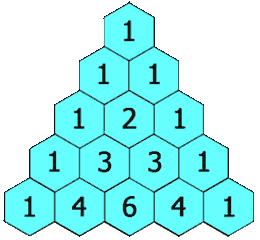
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: rowIndex = 3
输出: [1,3,3,1]
示例 2:
输入: rowIndex = 0
输出: [1]
示例 3:
输入: rowIndex = 1
输出: [1,1]
提示:
0 <= rowIndex <= 33
进阶:
你可以优化你的算法到 O(rowIndex) 空间复杂度吗?
Metadata
- Link: Pascal's Triangle II
- Difficulty: Easy
- Tag:
ArrayDynamic Programming
Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
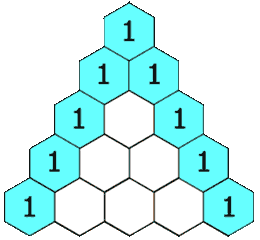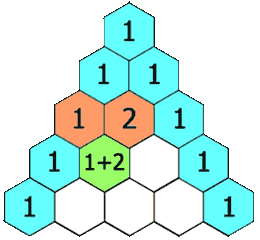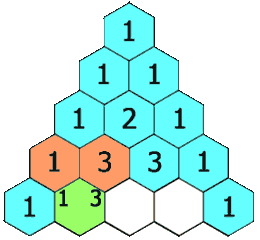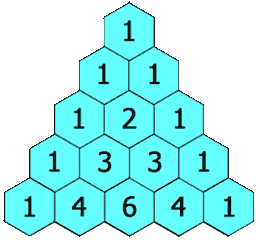
Example 1:
Input: rowIndex = 3
Output: [1,3,3,1]
Example 2:
Input: rowIndex = 0
Output: [1]
Example 3:
Input: rowIndex = 1
Output: [1,1]
Constraints:
0 <= rowIndex <= 33
Follow up: Could you optimize your algorithm to use only O(rowIndex) extra space?
Solution
最后更新: October 11, 2023