weekly-contest-294
A
Statement
Metadata
- Link: 字母在字符串中的百分比
- Difficulty: Easy
- Tag:
字符串
给你一个字符串 s 和一个字符 letter ,返回在 s 中等于 letter 字符所占的 百分比 ,向下取整到最接近的百分比。
示例 1:
输入:s = "foobar", letter = "o"
输出:33
解释:
等于字母 'o' 的字符在 s 中占到的百分比是 2 / 6 * 100% = 33% ,向下取整,所以返回 33 。
示例 2:
输入:s = "jjjj", letter = "k"
输出:0
解释:
等于字母 'k' 的字符在 s 中占到的百分比是 0% ,所以返回 0 。
提示:
1 <= s.length <= 100s由小写英文字母组成letter是一个小写英文字母
Metadata
- Link: Percentage of Letter in String
- Difficulty: Easy
- Tag:
String
Given a string s and a character letter, return the percentage of characters in s that equal letter rounded down to the nearest whole percent.
Example 1:
Input: s = "foobar", letter = "o"
Output: 33
Explanation:
The percentage of characters in s that equal the letter 'o' is 2 / 6 * 100% = 33% when rounded down, so we return 33.
Example 2:
Input: s = "jjjj", letter = "k"
Output: 0
Explanation:
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
Constraints:
1 <= s.length <= 100sconsists of lowercase English letters.letteris a lowercase English letter.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int percentageLetter(string s, char letter) {
int tot = s.length();
int cur = 0;
for (const char &c : s) {
if (c == letter) {
++cur;
}
}
return cur * 100 / tot;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 装满石头的背包的最大数量
- Difficulty: Medium
- Tag:
贪心数组排序
现有编号从 0 到 n - 1 的 n 个背包。给你两个下标从 0 开始的整数数组 capacity 和 rocks 。第 i 个背包最大可以装 capacity[i] 块石头,当前已经装了 rocks[i] 块石头。另给你一个整数 additionalRocks ,表示你可以放置的额外石头数量,石头可以往 任意 背包中放置。
请你将额外的石头放入一些背包中,并返回放置后装满石头的背包的 最大 数量。
示例 1:
输入:capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
输出:3
解释:
1 块石头放入背包 0 ,1 块石头放入背包 1 。
每个背包中的石头总数是 [2,3,4,4] 。
背包 0 、背包 1 和 背包 2 都装满石头。
总计 3 个背包装满石头,所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意,可能存在其他放置石头的方案同样能够得到 3 这个结果。
示例 2:
输入:capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
输出:3
解释:
8 块石头放入背包 0 ,2 块石头放入背包 2 。
每个背包中的石头总数是 [10,2,2] 。
背包 0 、背包 1 和背包 2 都装满石头。
总计 3 个背包装满石头,所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意,不必用完所有的额外石头。
提示:
n == capacity.length == rocks.length1 <= n <= 5 * 1041 <= capacity[i] <= 1090 <= rocks[i] <= capacity[i]1 <= additionalRocks <= 109
Metadata
- Link: Maximum Bags With Full Capacity of Rocks
- Difficulty: Medium
- Tag:
GreedyArraySorting
You have n bags numbered from 0 to n - 1. You are given two 0-indexed integer arrays capacity and rocks. The ith bag can hold a maximum of capacity[i] rocks and currently contains rocks[i] rocks. You are also given an integer additionalRocks, the number of additional rocks you can place in any of the bags.
Return the maximum number of bags that could have full capacity after placing the additional rocks in some bags.
Example 1:
Input: capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
Output: 3
Explanation:
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now [2,3,4,4].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
Example 2:
Input: capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
Output: 3
Explanation:
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now [10,2,2].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
Constraints:
n == capacity.length == rocks.length1 <= n <= 5 * 1041 <= capacity[i] <= 1090 <= rocks[i] <= capacity[i]1 <= additionalRocks <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maximumBags(vector<int> &capacity, vector<int> &rocks, int additionalRocks) {
auto need = vector<int>();
int n = capacity.size();
for (int i = 0; i < n; i++) {
need.push_back(capacity[i] - rocks[i]);
}
sort(need.begin(), need.end());
reverse(need.begin(), need.end());
int res = 0;
while (!need.empty()) {
int cur = need.back();
need.pop_back();
if (cur > additionalRocks) {
break;
}
additionalRocks -= cur;
++res;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 表示一个折线图的最少线段数
- Difficulty: Medium
- Tag:
几何数组数学数论排序
给你一个二维整数数组 stockPrices ,其中 stockPrices[i] = [dayi, pricei] 表示股票在 dayi 的价格为 pricei 。折线图 是一个二维平面上的若干个点组成的图,横坐标表示日期,纵坐标表示价格,折线图由相邻的点连接而成。比方说下图是一个例子:
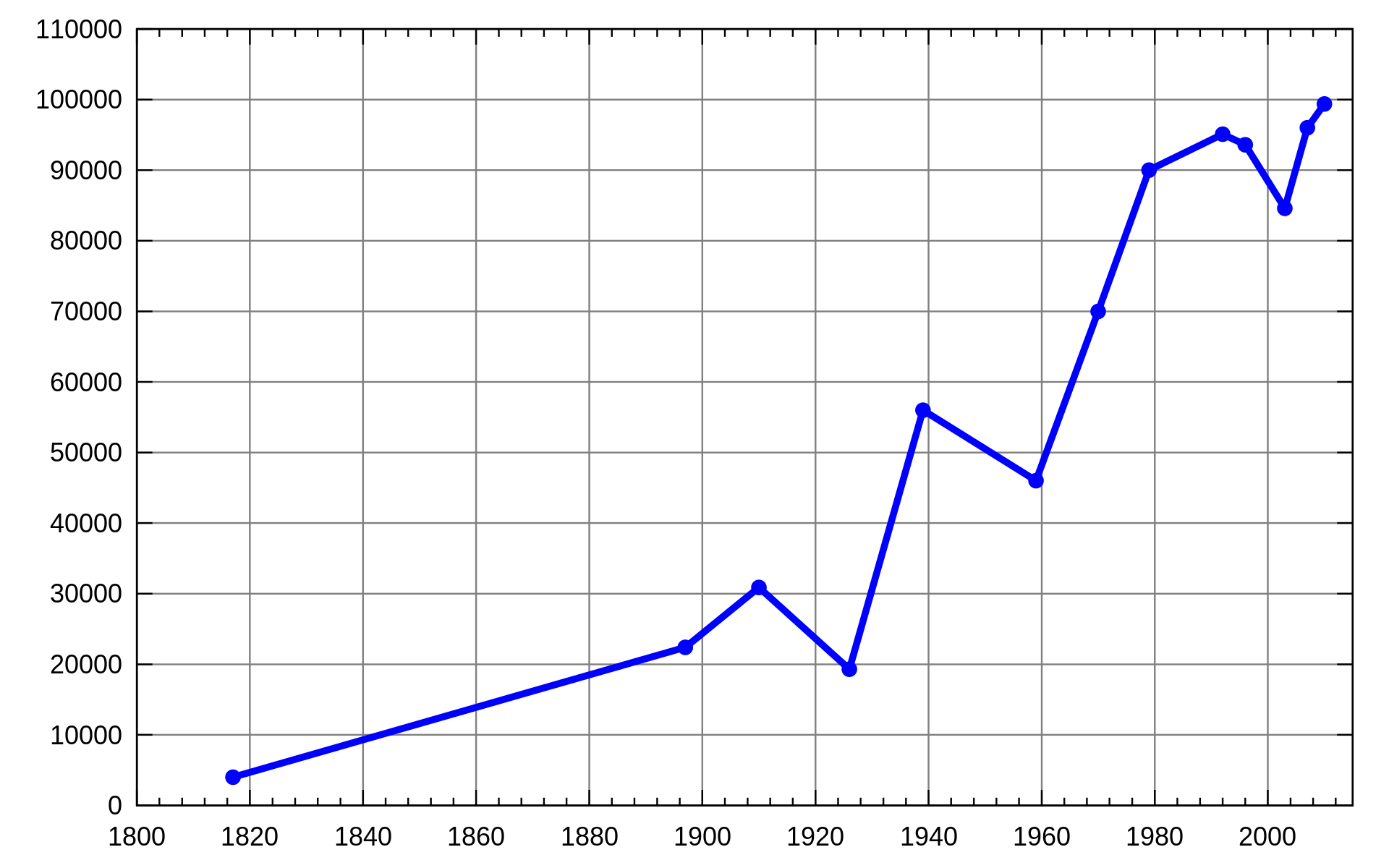
请你返回要表示一个折线图所需要的 最少线段数 。
示例 1:
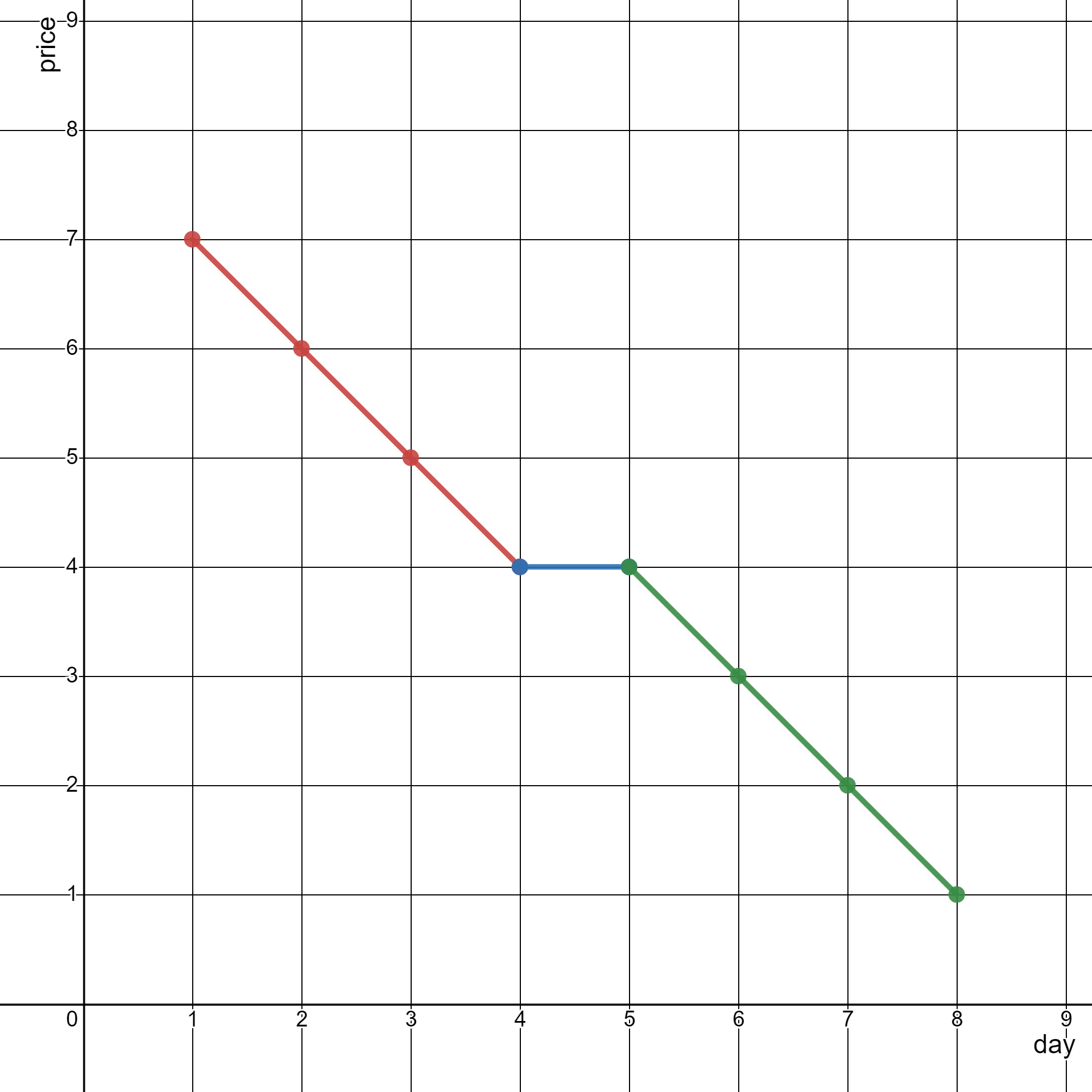
输入:stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出:3
解释:
上图为输入对应的图,横坐标表示日期,纵坐标表示价格。
以下 3 个线段可以表示折线图:
- 线段 1 (红色)从 (1,7) 到 (4,4) ,经过 (1,7) ,(2,6) ,(3,5) 和 (4,4) 。
- 线段 2 (蓝色)从 (4,4) 到 (5,4) 。
- 线段 3 (绿色)从 (5,4) 到 (8,1) ,经过 (5,4) ,(6,3) ,(7,2) 和 (8,1) 。
可以证明,无法用少于 3 条线段表示这个折线图。
示例 2:
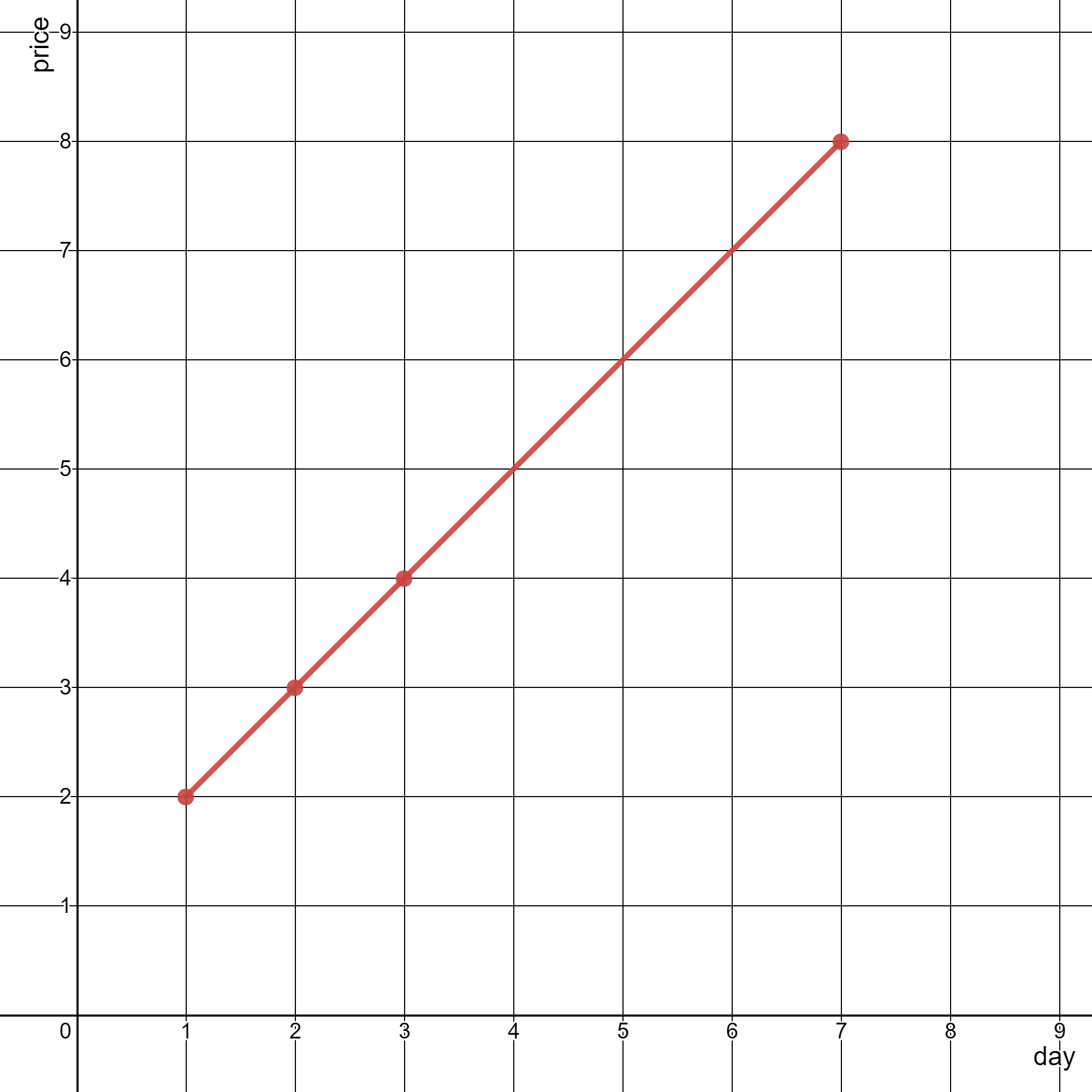
输入:stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出:1
解释:
如上图所示,折线图可以用一条线段表示。
提示:
1 <= stockPrices.length <= 105stockPrices[i].length == 21 <= dayi, pricei <= 109- 所有
dayi互不相同 。
Metadata
- Link: Minimum Lines to Represent a Line Chart
- Difficulty: Medium
- Tag:
GeometryArrayMathNumber TheorySorting
You are given a 2D integer array stockPrices where stockPrices[i] = [dayi, pricei] indicates the price of the stock on day dayi is pricei. A line chart is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:

Return the minimum number of lines needed to represent the line chart.
Example 1:

Input: stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
Output: 3
Explanation:
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.
Example 2:

Input: stockPrices = [[3,4],[1,2],[7,8],[2,3]]
Output: 1
Explanation:
As shown in the diagram above, the line chart can be represented with a single line.
Constraints:
1 <= stockPrices.length <= 105stockPrices[i].length == 21 <= dayi, pricei <= 109- All
dayiare distinct.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minimumLines(vector<vector<int>> &s) {
int n = s.size();
if (n == 1) {
return 0;
}
if (n <= 2) {
return 1;
}
sort(s.begin(), s.end(), [&](const vector<int> &a, const vector<int> &b) {
return a[0] < b[0];
});
const auto ok = [](vector<int> a, vector<int> b, vector<int> c) {
ll aa = 1ll * (b[1] - a[1]) * (c[0] - a[0]);
ll bb = 1ll * (b[0] - a[0]) * (c[1] - a[1]);
return aa == bb;
};
int res = 1;
int l = 0;
for (int i = 2; i < n; i++) {
if (ok(s[l], s[l + 1], s[i])) {
continue;
}
l = i - 1;
++res;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 巫师的总力量和
- Difficulty: Hard
- Tag:
栈数组前缀和单调栈
作为国王的统治者,你有一支巫师军队听你指挥。
给你一个下标从 0 开始的整数数组 strength ,其中 strength[i] 表示第 i 位巫师的力量值。对于连续的一组巫师(也就是这些巫师的力量值是 strength 的 子数组),总力量 定义为以下两个值的 乘积 :
- 巫师中 最弱 的能力值。
- 组中所有巫师的个人力量值 之和 。
请你返回 所有 巫师组的 总 力量之和。由于答案可能很大,请将答案对 109 + 7 取余 后返回。
子数组 是一个数组里 非空 连续子序列。
示例 1:
输入:strength = [1,3,1,2]
输出:44
解释:以下是所有连续巫师组:
- [1,3,1,2] 中 [1] ,总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
- [1,3,1,2] 中 [3] ,总力量值为 min([3]) * sum([3]) = 3 * 3 = 9
- [1,3,1,2] 中 [1] ,总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
- [1,3,1,2] 中 [2] ,总力量值为 min([2]) * sum([2]) = 2 * 2 = 4
- [1,3,1,2] 中 [1,3] ,总力量值为 min([1,3]) * sum([1,3]) = 1 * 4 = 4
- [1,3,1,2] 中 [3,1] ,总力量值为 min([3,1]) * sum([3,1]) = 1 * 4 = 4
- [1,3,1,2] 中 [1,2] ,总力量值为 min([1,2]) * sum([1,2]) = 1 * 3 = 3
- [1,3,1,2] 中 [1,3,1] ,总力量值为 min([1,3,1]) * sum([1,3,1]) = 1 * 5 = 5
- [1,3,1,2] 中 [3,1,2] ,总力量值为 min([3,1,2]) * sum([3,1,2]) = 1 * 6 = 6
- [1,3,1,2] 中 [1,3,1,2] ,总力量值为 min([1,3,1,2]) * sum([1,3,1,2]) = 1 * 7 = 7
所有力量值之和为 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44 。
示例 2:
输入:strength = [5,4,6]
输出:213
解释:以下是所有连续巫师组:
- [5,4,6] 中 [5] ,总力量值为 min([5]) * sum([5]) = 5 * 5 = 25
- [5,4,6] 中 [4] ,总力量值为 min([4]) * sum([4]) = 4 * 4 = 16
- [5,4,6] 中 [6] ,总力量值为 min([6]) * sum([6]) = 6 * 6 = 36
- [5,4,6] 中 [5,4] ,总力量值为 min([5,4]) * sum([5,4]) = 4 * 9 = 36
- [5,4,6] 中 [4,6] ,总力量值为 min([4,6]) * sum([4,6]) = 4 * 10 = 40
- [5,4,6] 中 [5,4,6] ,总力量值为 min([5,4,6]) * sum([5,4,6]) = 4 * 15 = 60
所有力量值之和为 25 + 16 + 36 + 36 + 40 + 60 = 213 。
提示:
1 <= strength.length <= 1051 <= strength[i] <= 109
Metadata
- Link: Sum of Total Strength of Wizards
- Difficulty: Hard
- Tag:
StackArrayPrefix SumMonotonic Stack
As the ruler of a kingdom, you have an army of wizards at your command.
You are given a 0-indexed integer array strength, where strength[i] denotes the strength of the ith wizard. For a contiguous group of wizards (i.e. the wizards' strengths form a subarray of strength), the total strength is defined as the product of the following two values:
- The strength of the weakest wizard in the group.
- The total of all the individual strengths of the wizards in the group.
Return the sum of the total strengths of all contiguous groups of wizards. Since the answer may be very large, return it modulo 109 + 7.
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
Input: strength = [1,3,1,2]
Output: 44
Explanation: The following are all the contiguous groups of wizards:
- [1] from [1,3,1,2] has a total strength of min([1]) * sum([1]) = 1 * 1 = 1
- [3] from [1,3,1,2] has a total strength of min([3]) * sum([3]) = 3 * 3 = 9
- [1] from [1,3,1,2] has a total strength of min([1]) * sum([1]) = 1 * 1 = 1
- [2] from [1,3,1,2] has a total strength of min([2]) * sum([2]) = 2 * 2 = 4
- [1,3] from [1,3,1,2] has a total strength of min([1,3]) * sum([1,3]) = 1 * 4 = 4
- [3,1] from [1,3,1,2] has a total strength of min([3,1]) * sum([3,1]) = 1 * 4 = 4
- [1,2] from [1,3,1,2] has a total strength of min([1,2]) * sum([1,2]) = 1 * 3 = 3
- [1,3,1] from [1,3,1,2] has a total strength of min([1,3,1]) * sum([1,3,1]) = 1 * 5 = 5
- [3,1,2] from [1,3,1,2] has a total strength of min([3,1,2]) * sum([3,1,2]) = 1 * 6 = 6
- [1,3,1,2] from [1,3,1,2] has a total strength of min([1,3,1,2]) * sum([1,3,1,2]) = 1 * 7 = 7
The sum of all the total strengths is 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44.
Example 2:
Input: strength = [5,4,6]
Output: 213
Explanation: The following are all the contiguous groups of wizards:
- [5] from [5,4,6] has a total strength of min([5]) * sum([5]) = 5 * 5 = 25
- [4] from [5,4,6] has a total strength of min([4]) * sum([4]) = 4 * 4 = 16
- [6] from [5,4,6] has a total strength of min([6]) * sum([6]) = 6 * 6 = 36
- [5,4] from [5,4,6] has a total strength of min([5,4]) * sum([5,4]) = 4 * 9 = 36
- [4,6] from [5,4,6] has a total strength of min([4,6]) * sum([4,6]) = 4 * 10 = 40
- [5,4,6] from [5,4,6] has a total strength of min([5,4,6]) * sum([5,4,6]) = 4 * 15 = 60
The sum of all the total strengths is 25 + 16 + 36 + 36 + 40 + 60 = 213.
Constraints:
1 <= strength.length <= 1051 <= strength[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int mod = 1e9 + 7;
struct node {
int x, l, r;
ll GetSum(const vector<ll> &suffix_sum) {
ll ans = 0;
ans += 1ll * x * (suffix_sum[l] - suffix_sum[r + 1] + mod) % mod;
ans %= mod;
return ans;
}
ll GetBaseSum() {
return 1ll * x * (r - l + 1);
}
};
class Solution {
public:
int totalStrength(vector<int> &a) {
int n = (int)a.size();
vector<vector<ll>> suffix_sum(2, vector<ll>(n + 5, 0));
for (int i = n; i >= 1; i--) {
suffix_sum[0][i] = (suffix_sum[0][i + 1] + a[i - 1]) % mod;
}
for (int i = n; i >= 1; i--) {
suffix_sum[1][i] = (suffix_sum[1][i + 1] + suffix_sum[0][i]) % mod;
}
vector<node> v;
ll sum = 0;
ll base_sum = 0;
ll res = 0;
for (int i = 0; i < n; i++) {
auto t = node();
t.x = a[i];
t.l = i + 1;
t.r = i + 1;
while (!v.empty()) {
if (v.back().x < t.x) {
break;
}
sum = (sum - v.back().GetSum(suffix_sum[1]) + mod) % mod;
base_sum = (base_sum - v.back().GetBaseSum() + mod) % mod;
t.l = v.back().l;
v.pop_back();
}
v.push_back(t);
sum = (sum + t.GetSum(suffix_sum[1])) % mod;
base_sum = (base_sum + t.GetBaseSum()) % mod;
res = (res + sum) % mod;
res -= 1ll * base_sum * suffix_sum[0][i + 2] % mod;
res += mod;
res %= mod;
}
return int(res);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif