weekly-contest-298

A

Statement

简体中文English

Metadata

Link: 兼具大小写的最好英文字母
Difficulty: Easy
Tag: 数组

给你一个由英文字母组成的字符串 s ，请你找出并返回 s 中的最好英文字母。返回的字母必须为大写形式。如果不存在满足条件的字母，则返回一个空字符串。

最好英文字母的大写和小写形式必须都在 s 中出现。

英文字母 b 比另一个英文字母 a 更好的前提是：英文字母表中，b 在 a 之后出现。

示例 1：

输入：s = "lEeTcOdE"
输出："E"
解释：
字母 'E' 是唯一一个大写和小写形式都出现的字母。

示例 2：

输入：s = "arRAzFif"
输出："R"
解释：
字母 'R' 是大写和小写形式都出现的最好英文字母。
注意 'A' 和 'F' 的大写和小写形式也都出现了，但是 'R' 比 'F' 和 'A' 更好。

示例 3：

输入：s = "AbCdEfGhIjK"
输出：""
解释：
不存在大写和小写形式都出现的字母。

提示：

1 <= s.length <= 1000
s 由小写和大写英文字母组成

Metadata

Link: Greatest English Letter in Upper and Lower Case
Difficulty: Easy
Tag: Array

Given a string of English letters s, return the greatest English letter which occurs as both a lowercase and uppercase letter in s. The returned letter should be in uppercase. If no such letter exists, return an empty string.

An English letter b is greater than another letter a if b appears after a in the English alphabet.

Example 1:

Input: s = "lEeTcOdE"
Output: "E"
Explanation:
The letter 'E' is the only letter to appear in both lower and upper case.

Example 2:

Input: s = "arRAzFif"
Output: "R"
Explanation:
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.

Example 3:

Input: s = "AbCdEfGhIjK"
Output: ""
Explanation:
There is no letter that appears in both lower and upper case.

Constraints:

1 <= s.length <= 1000
s consists of lowercase and uppercase English letters.

Solution

C++

#include <bits/stdc++.h>
#include <cctype>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    string greatestLetter(string s) {
        auto f = vector<int>(30, 0);
        for (auto &c : s) {
            if (islower(c)) {
                f[c - 'a'] |= 2;
            } else if (isupper(c)) {
                f[c - 'A'] |= 4;
            }
        }

        for (int i = 26; i >= 0; i--) {
            if (f[i] == 6) {
                return string(1, 'A' + i);
            }
        }

        return "";
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 个位数字为 K 的整数之和
Difficulty: Medium
Tag: 数学

给你两个整数 num 和 k ，考虑具有以下属性的正整数多重集：

每个整数个位数字都是 k 。
所有整数之和是 num 。

返回该多重集的最小大小，如果不存在这样的多重集，返回 -1 。

注意：

多重集与集合类似，但多重集可以包含多个同一整数，空多重集的和为 0 。
个位数字 是数字最右边的数位。

示例 1：

输入：num = 58, k = 9
输出：2
解释：
多重集 [9,49] 满足题目条件，和为 58 且每个整数的个位数字是 9 。
另一个满足条件的多重集是 [19,39] 。
可以证明 2 是满足题目条件的多重集的最小长度。

示例 2：

输入：num = 37, k = 2
输出：-1
解释：个位数字为 2 的整数无法相加得到 37 。

示例 3：

输入：num = 0, k = 7
输出：0
解释：空多重集的和为 0 。

提示：

0 <= num <= 3000
0 <= k <= 9

Metadata

Link: Sum of Numbers With Units Digit K
Difficulty: Medium
Tag: Math

Given two integers num and k, consider a set of positive integers with the following properties:

The units digit of each integer is k.
The sum of the integers is num.

Return the minimum possible size of such a set, or -1 if no such set exists.

Note:

The set can contain multiple instances of the same integer, and the sum of an empty set is considered 0.
The units digit of a number is the rightmost digit of the number.

Example 1:

Input: num = 58, k = 9
Output: 2
Explanation:
One valid set is [9,49], as the sum is 58 and each integer has a units digit of 9.
Another valid set is [19,39].
It can be shown that 2 is the minimum possible size of a valid set.

Example 2:

Input: num = 37, k = 2
Output: -1
Explanation: It is not possible to obtain a sum of 37 using only integers that have a units digit of 2.

Example 3:

Input: num = 0, k = 7
Output: 0
Explanation: The sum of an empty set is considered 0.

Constraints:

0 <= num <= 3000
0 <= k <= 9

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int minimumNumbers(int num, int k) {
        if (num == 0) {
            return 0;
        }

        if (num < k) {
            return -1;
        }

        int sum = 0;
        for (int i = 1; i <= 10; i++) {
            sum += k;
            if (num % 10 == sum % 10 && sum <= num) {
                return i;
            }
        }

        return -1;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 小于等于 K 的最长二进制子序列
Difficulty: Medium
Tag:

给你一个二进制字符串 s 和一个正整数 k 。

请你返回 s 的最长子序列，且该子序列对应的 二进制 数字小于等于 k 。

注意：

子序列可以有 前导 0 。
空字符串视为 0 。
子序列 是指从一个字符串中删除零个或者多个字符后，不改变顺序得到的剩余字符序列。

示例 1：

输入：s = "1001010", k = 5
输出：5
解释：s 中小于等于 5 的最长子序列是 "00010" ，对应的十进制数字是 2 。
注意 "00100" 和 "00101" 也是可行的最长子序列，十进制分别对应 4 和 5 。
最长子序列的长度为 5 ，所以返回 5 。

示例 2：

输入：s = "00101001", k = 1
输出：6
解释："000001" 是 s 中小于等于 1 的最长子序列，对应的十进制数字是 1 。
最长子序列的长度为 6 ，所以返回 6 。

提示：

1 <= s.length <= 1000
s[i] 要么是 '0' ，要么是 '1' 。
1 <= k <= 10⁹

Metadata

Link: Longest Binary Subsequence Less Than or Equal to K
Difficulty: Medium
Tag:

You are given a binary string s and a positive integer k.

Return the length of the longest subsequence of s that makes up a binary number less than or equal to k.

Note:

The subsequence can contain leading zeroes.
The empty string is considered to be equal to 0.
A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.

Example 1:

Input: s = "1001010", k = 5
Output: 5
Explanation: The longest subsequence of s that makes up a binary number less than or equal to 5 is "00010", as this number is equal to 2 in decimal.
Note that "00100" and "00101" are also possible, which are equal to 4 and 5 in decimal, respectively.
The length of this subsequence is 5, so 5 is returned.

Example 2:

Input: s = "00101001", k = 1
Output: 6
Explanation: "000001" is the longest subsequence of s that makes up a binary number less than or equal to 1, as this number is equal to 1 in decimal.
The length of this subsequence is 6, so 6 is returned.

Constraints:

1 <= s.length <= 1000
s[i] is either '0' or '1'.
1 <= k <= 10⁹

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <numeric>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int longestSubsequence(string s, int k) {
        int len = int(s.size());
        auto f = vector<int>(len + 1, 0);

        for (int i = 0; i < len; i++) {
            if (s[i] == '0') {
                f[i] = 1;
            }
        }

        ll sum = 0, base = 1;
        for (int i = len - 1; i >= 0 && base <= k; i--) {
            if (s[i] == '1') {
                if (sum + base <= k) {
                    sum += base;
                    f[i] = 1;
                } else {
                    break;
                }
            }

            base <<= 1;
        }

        return accumulate(f.begin(), f.end(), 0);
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 卖木头块
Difficulty: Hard
Tag: 回溯

给你两个整数 m 和 n ，分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ，其中 prices[i] = [h_i, w_i, price_i] 表示你可以以 price_i 元的价格卖一块高为 h_i 宽为 w_i 的矩形木块。

每一次操作中，你必须按下述方式之一执行切割操作，以得到两块更小的矩形木块：

沿垂直方向按高度完全切割木块，或
沿水平方向按宽度完全切割木块

在将一块木块切成若干小木块后，你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你不能旋转切好后木块的高和宽。

请你返回切割一块大小为 m x n 的木块后，能得到的最多钱数。

注意你可以切割木块任意次。

示例 1：

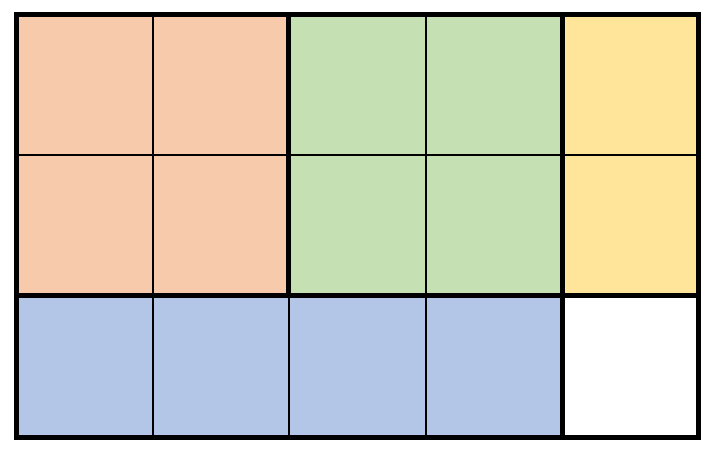
输入：m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出：19
解释：上图展示了一个可行的方案。包括：
- 2 块 2 x 2 的小木块，售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块，售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。

示例 2：

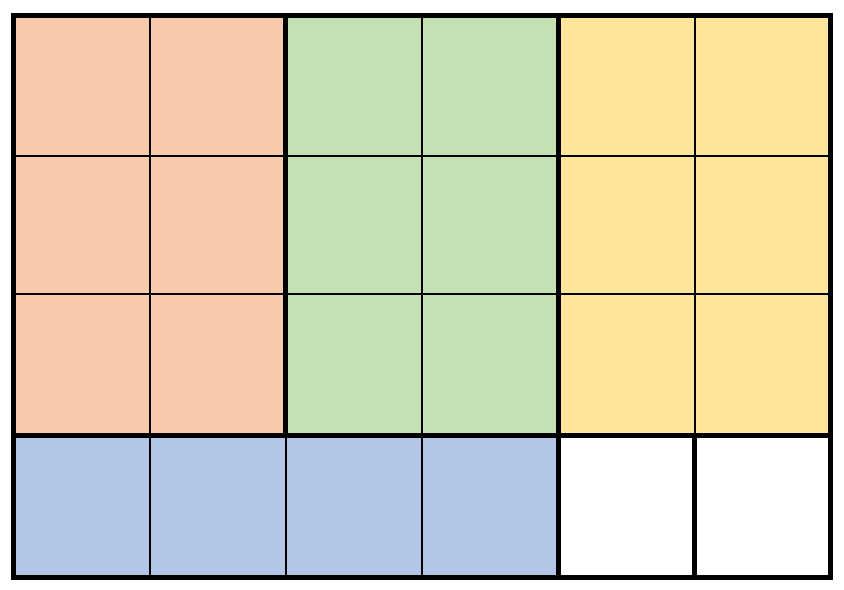
输入：m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出：32
解释：上图展示了一个可行的方案。包括：
- 3 块 3 x 2 的小木块，售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。

提示：

1 <= m, n <= 200
1 <= prices.length <= 2 * 10⁴
prices[i].length == 3
1 <= h_i <= m
1 <= w_i <= n
1 <= price_i <= 10⁶
所有 (h_i, w_i) 互不相同 。

Metadata

Link: Selling Pieces of Wood
Difficulty: Hard
Tag: Backtracking

You are given two integers m and n that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array prices, where prices[i] = [h_i, w_i, price_i] indicates you can sell a rectangular piece of wood of height h_i and width w_i for price_i dollars.

To cut a piece of wood, you must make a vertical or horizontal cut across the entire height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to prices. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you cannot rotate a piece to swap its height and width.

Return the maximum money you can earn after cutting an m x n piece of wood.

Note that you can cut the piece of wood as many times as you want.

Example 1:

Input: m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
Output: 19
Explanation: The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 * 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 * 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.

Example 2:

Input: m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
Output: 32
Explanation: The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 * 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 * 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.

Constraints:

1 <= m, n <= 200
1 <= prices.length <= 2 * 10⁴
prices[i].length == 3
1 <= h_i <= m
1 <= w_i <= n
1 <= price_i <= 10⁶
All the shapes of wood (h_i, w_i) are pairwise distinct.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    long long sellingWood(int m, int n, vector<vector<int>> &prices) {
        auto f = vector<vector<ll>>(m + 1, vector<ll>(n + 1, 0));
        for (auto &p : prices) {
            f[p[0]][p[1]] = p[2];
        }

        while (true) {
            bool change = false;

            for (int i = 1; i <= m; i++) {
                for (int j = 1; j <= n; j++) {
                    for (int k = 1; k < j; k++) {
                        if (f[i][j - k] + f[i][k] > f[i][j]) {
                            change = true;
                            f[i][j] = f[i][j - k] + f[i][k];
                        }
                    }
                }
            }

            for (int j = 1; j <= n; j++) {
                for (int i = 1; i <= m; i++) {
                    for (int k = 1; k < i; k++) {
                        if (f[i - k][j] + f[k][j] > f[i][j]) {
                            change = true;
                            f[i][j] = f[i - k][j] + f[k][j];
                        }
                    }
                }
            }

            if (!change) {
                break;
            }
        }

        return f[m][n];
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023